22、有一列焦点为F_n的抛物线C_n:y²=4ⁿ·x，过F_n作倾斜角为45°的直线与相交于A_n和B_n(A_n在x轴的上方，B_n在x轴的下方)

(1)求证：坐标原点O与A₁、A₂、A₃、…、A_n、…共线

(2)若记△A_nOB_n的面积为S_n，证明：|S_n|是等比数列。

[答案]

21、已知点F(1，0)，直线：x=2，设动点P到直线的距离为d，已知|PF|=且。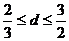

(1)求动点P的轨迹方程；

(2)若，求向量的夹角。

20、已知空间四边形ABCD的各边长分别为AB=，AC=AD=BC=BD=CD=2，E，F分别是AB，CD的中点(如图所示)

(1)求异面直线AB与CD间的距离；

(2)在线段EF上是否存在一点O，使O到A、B、C、D四点相等？若不存在，则说明理由；若存在，则求出此距离。

19、甲、乙两名射击运动员，甲命中10环的概率为，乙命中10环的概率为P，若他们各射击两次，甲比乙命中10环次数多的概率恰好等于，试求P的值。

18、求曲线在直线x=1右侧部的最低点(即此点的纵坐标最小)的坐标。

17、求函数的值域。

16、一动圆与两圆(x+4)²+y²=25和(x-4)²+y²=4都外切，则动圆圆心M的轨迹方程是　　　 。

15、函数的最小正周期是　　　 。

14、一个容量为n的样本分成若干组，已知某组的频率和频数分别为0.25和30，则n=　　　　 。

13、方程的解集是　　　　　 。