
1. 若关于x的不等式x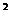 -4x≥m对任意 x∈(0,1
-4x≥m对任意 x∈(0,1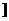 恒成立,则 m的取值范围为
恒成立,则 m的取值范围为
例1 求下列二次函数的解析式
(1) 图像顶点的坐标为(2,-1),与y轴交点坐标为(0,11);
(2) 已知函数f(x)满足f(0)=1,且f(x+1)-f(x)=2x;
(3) f (2)=0,f(-1)=0且过点(0,4)求f(x).
例2 已知函数 ,当
,当 时,
时,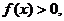 当
当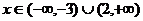 时,
时, 。(1)求
。(1)求 在
在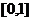 内的值域。
内的值域。
(2)若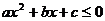 的解集为R,求实数c的取值范围。
的解集为R,求实数c的取值范围。
例3 已知函数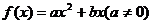 满足条件
满足条件 且方程
且方程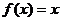 有等根,(1)求
有等根,(1)求 的解析式;(2)是否存在实数
的解析式;(2)是否存在实数 ,使
,使 的定义域和值域分别是
的定义域和值域分别是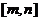 和
和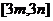 ?如果存在,求出
?如果存在,求出 的值;若不存在说明理由。
的值;若不存在说明理由。
例4已知关于x的方程mx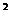 +(m-3)x+1=0 ①若存在正根,求实数m的取值范围 ②2个正根m的取值范围 ③一正一负根m的取值范围 ④2个负根的m的取值范围
+(m-3)x+1=0 ①若存在正根,求实数m的取值范围 ②2个正根m的取值范围 ③一正一负根m的取值范围 ④2个负根的m的取值范围
1、已知二次函数 的对称轴方程为x=2,则在f(1),f(2),f(3),f(4),f(5)中,相等的两个值为
,最大值为
。
的对称轴方程为x=2,则在f(1),f(2),f(3),f(4),f(5)中,相等的两个值为
,最大值为
。
2函数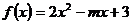 ,当
,当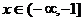 时,是减函数,则实数m的取值范围是
。
时,是减函数,则实数m的取值范围是
。
3函数 的定义域为R,则实数
的定义域为R,则实数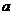 的取值范围是
的取值范围是 
4已知不等式 的解集为
的解集为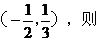

5若函数f(x)=(x+a)(bx+2a) (常数a、b∈R) 是偶函数,且他的值域为(-∞,4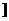 ,则f(x)=
,则f(x)=
6 设二次函数y=f(x)的最大值为13,且f(3)= f(-1)=5,则f(x)=
7已知二次函数 的值域为
的值域为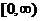 ,则实数
,则实数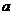 =
=
2、 二次函数的图像和性质
二次函数 的图像是一条抛物线,对称轴的方程为
顶点坐标是(
)
。
的图像是一条抛物线,对称轴的方程为
顶点坐标是(
)
。
(1)当 时,抛物线的开口
,函数在
上递减,在 上递增,当
时,抛物线的开口
,函数在
上递减,在 上递增,当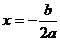 时,函数有最 值为
时,函数有最 值为
(2)当 时,抛物线的开口 ,函数在
上递减,在
上递增,当
时,抛物线的开口 ,函数在
上递减,在
上递增,当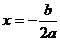 时,函数有最 值 为
时,函数有最 值 为
。
(3)二次函数
当
时,恒有  ,
,
当
时,恒有  。
。
(4)二次函数 ,当
,当 时,图像与
时,图像与  x轴有两个交点,
x轴有两个交点,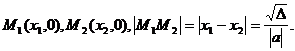
1、 二次函数的解析式
(1)一般式:
(2)顶点式:
(3)双根式:
求二次函数解析式的方法:
1已知 时,宜用一般式
2已知 时,常使用顶点式
3已知 时,用双根式更方便
由于二次函数与二次方程、二次不等式之间有着紧密的联系,加上三次函数的导数是二次函数,因此二次函数在高中数学中应用十分广泛,一直是高考的热点,特别是借助二次函数模型考查考生的代数推理问题是高考的热点和难点,另外二次函数的应用问题也是2010年高考的热点。
3、 掌握二次函数、二次方程、二次不等式(三个二次)之间的紧密关系,提高解综合问题的能力。
2、 掌握二次函数的对称性和单调性,会求二次函数在给定区间上的最值
1、 掌握二次函数的概念、图像特征
7、(12分)在一批野生正常翅(h)果蝇中,出现少数毛翅(H)的显性突变个体,这些突变个体在培养过程中可能因某种原因而恢复正常翅,这种突变成毛翅后又恢复为正常翅的个体称为回复体。回复体出现的原因可能有两种;一是因为基因H又突变为h;二是由于体内另一对基因RR突变为rr,从而抑制H基因的表达(R、r基因本身并没有控制具体性状,其中RR、Rr基因组合不影响H、h基因的表达,只有rr基因组合时才会抑制H基因的表达)。由于第一种原因出现的回复体称为“真回复体”,第二种原因出现的回复体称为“假回复体”。请分析回答:
(1)表现正常翅果蝇(包括真、假回复体)的基因型可能为: hhRR、HHrr、Hhrr (2分) 以及hhRr、hhrr;表现毛翅果蝇的基因型可能为 HHRR、HhRR、 HhRr (2分) 以及HHRr。
(2)现获得一批纯合的果蝇回复体,欲判断其基因型是HHrr还是hhRR,请完成以下简单的实验方案(写出简单的实验思路,预测实验结果并得出结论)。
①实验思路:让这批纯合的果蝇回复体与 纯合野生正常翅果蝇 (1分) 杂交,观察子代果蝇的性状表现。
②预测实验结果并得出相应结论:
若子代果蝇全为正常翅,则这批果蝇的基因型为 hhRR ; (1分)
若子代果蝇全为毛翅,则这批果蝇的基因型为 HHrr。 (1分)
(3)实验结果表明这批果蝇属于假回复体,请利用这些果蝇及纯合野生正常翅果蝇进行杂交实验,以判断这两对基因是位于同一对染色体上还是位于不同对的染色体上。(写出实验步骤,预测实验结果并得出结论)。
①实验步骤(写出要点即可):
让这些果蝇与纯合野生正常翅果蝇进行杂交获得F1;(1分)让F1果蝇雌雄个体自由交配获得F2;(1分)
观察F2果蝇的性状表现,并统计其性状分离比。(1分)
②预测实验结果并得出相应结论:
若F2果蝇中毛翅与正常翅的比为9:7,则这两对基因位于不同对的染色体上;(1分)
若F2果蝇中毛翅与正常翅的比不为9:7,则这两对基因位于同一对染色体上;(1分)
[解析](1)由于rr基因会抑制H基因的表达,故表现正常翅果蝇(包括真、假回复体)的基因型可能为:hhRR、HHrr、Hhrr、hhRr、hhrr;由于RR、Rr基因组合不影响H、h基因的表达,故表现毛翅果蝇的基因型可能为HHRR、HhRR、 HhRr、HHRr。
(2)欲判断一批纯合的果蝇回复体,基因型是HHrr还是hhRR,在选择与其交配的果蝇时,应注意使两种交配情况下所产生的子代果蝇性状不相同,这样方可判断出这批纯合的果蝇回复体的基因型。
(3)如果两对基因是位于不同对的染色体上,则遵循基因的自由组合规律,否则不遵循,所以可用这些果蝇与纯合野生正常翅果蝇进行杂交获得F1,然后让F1果蝇雌雄个体自由交配获得F2,观察F2果蝇的性状表现并统计其性状分离比,看是否符合孟德尔的基因自由组合规律。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com