
18.(12分)已知不等式mx2-2mx+m-1<0。
(1)若对所有的实数x不等式恒成立,求m的取值范围;
(2)设不等式对于满足|m|<2的一切m的值都成立,求x的取值范围。
16.(12分)已知函数f(x)= sinωxcosωx-cos2ωx-
sinωxcosωx-cos2ωx- (x∈R,ω>0)。
(x∈R,ω>0)。
(1)若f (x)的图象中相邻的两条对称轴之间的距离不小于
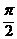 ,求ω的取值范围;
,求ω的取值范围;
(2)若f (x)的最小正周期为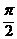 ,求函数f (x)的最大值,并且求出使f (x)取得最大值的x的集合。
,求函数f (x)的最大值,并且求出使f (x)取得最大值的x的集合。
17 .(12分)已知向量
.(12分)已知向量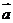 =(
=( ,-1),
,-1), =(
=( ,
, )且存在实数k和t使
)且存在实数k和t使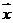 =
=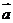 +(t2-3)
+(t2-3) ,
, =-k
=-k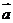 + t
+ t ,若
,若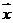 ⊥
⊥ ,试求
,试求 的最小值。
的最小值。
15.函数f(x)= 为奇函数,则实数a的取值
为奇函数,则实数a的取值 范围是
;
范围是
;
14.已知向量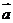 与
与 的夹角为120º,若向量
的夹角为120º,若向量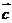 =
=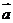 +
+ ,且
,且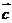 ⊥
⊥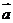 ,则
,则 的值为 ;
的值为 ;
13.把函 数
数 的图象向右平移
的图象向右平移 个单位,再把所得图象上各点的横坐标变为原来的
个单位,再把所得图象上各点的横坐标变为原来的 (纵坐标不变),则所得图象的解
(纵坐标不变),则所得图象的解 析式为
;
析式为
;
12.已知点P(x,y)满足条件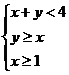 ,则x2+y2的值域为 ;
,则x2+y2的值域为 ;
11.设等差数列 的前
的前 项和为
项和为 ,若
,若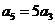 则
则 ;
;
10.定义在R上的偶函数f(x)满足f(x+2)=f(x),且f(x)在[-3,-2]上是减函数,又α、β是锐角三角形的两个内角,则
A、f(sinα)>f(sinβ) B、f(cosα)<f(cosβ)
C、f(sinα)<f(cosβ) D、f(sinα)>f(cosβ)
9. 设函数f(x)定义如下表,数列{xn}满足x0=5,且对任意的自然数n均有xn+1=f(xn),则x2009等于
设函数f(x)定义如下表,数列{xn}满足x0=5,且对任意的自然数n均有xn+1=f(xn),则x2009等于
|
x |
1 |
2 |
3 |
4 |
5 |
|
f(x) |
4 |
1 |
3 |
5 |
2 |
A、1 B、2 C、4 D、5
8.在⊿ABC中,若(a-c•cosB)sinB=(b-c•cosA)sinA,则这个三角形是
A、等腰三角形 B、直角三角形
C、等腰或直角三角形 D、等腰直角三角形
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com