
6、二战期间的一个早晨,英军指挥部接到各雷达站的报告,说雷达受到了来自东方奇怪信号的干扰,这种干扰方向与太阳移动的方向一致,而且只出现在白天,下列原因中比较合乎情理的解释是 ( )
A.德军使用的一种秘密武器. B.雷达本身的故障
C.外界杂波的干扰. D.太阳活动的影响
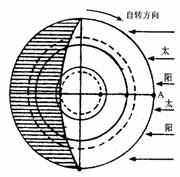
读右图(阴影部分指地球的夜半球),回答4---5小题
4.这一天的节气是
A.春分 B.夏至
C.秋分 D.冬至
5.某地(700N,1350E)当天的昼长时间为
A.0小时 B.12小时 C.16小时 D.24小时
3.2002年12月10日伦敦格林尼治时间20:00进行了一场欧洲冠军联赛的比赛,电视台对此比赛进行了现场直播,那么电视机前的中国观众在什么时间看到了比赛的开球?
 A.12月10日12:00 B.12月11日 4:00
A.12月10日12:00 B.12月11日 4:00
C.12月9日4:00 D.12月9日12:00
2.被认为是太阳活动强弱的标志是
A.太阳黑子的大小和多少 B.太阳耀斑出现的频率和大小
C.太阳风的剧烈程度 D.地球的“磁暴”现象
1.下列天体系统中,和河外星系属于同级系统的是:
A.地月系 B.太阳系 C.银河系 D.总星系
|
数列 (一)数列的概念 涉及的数列及表示 1.数列的定义 2.数列与函数的关系 3.数列的表示法 (1)列举法 (2)图示法 (3)通项公式法 (4)递推公式法 |
典型例题
例1.数列  共有__________项.
共有__________项.
分析:数一个数列的项数都是从1开始的,找项与项数的关系关键是找首项与1的关系.
解:已知数列的项数与数列
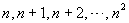 的项数相同,
的项数相同,
又 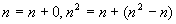 ,所以又与数列
,所以又与数列
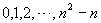 的项数相同.
的项数相同.
因为  共有
共有
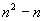 个数,所以
个数,所以
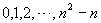 共有
共有
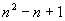 个数.
个数.
因此 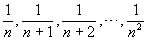 有
有
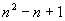 个数.
个数.
说明:数清项数是解决数列问题的首要问题,在有穷数列中,数列的末项未必是数列的第
 项,即有穷数列的项数未必是
项,即有穷数列的项数未必是
 .一定要区分有穷数列的末项与通项.
.一定要区分有穷数列的末项与通项.
例2.已知数列 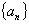 中,
中,
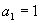 ,对任意
,对任意
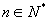 ,
,
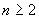 ,都有
,都有
 则
则
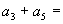 ______.
______.
分析:已知条件 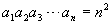 表示了无数个等式:
表示了无数个等式:
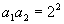 ,
,
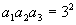 ,
,
 ,再加上
,再加上
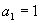 这一条件便确定了这个数列,即可递推求出数列的各项.
这一条件便确定了这个数列,即可递推求出数列的各项.
解:令 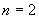 ,得
,得
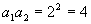 ,
,
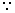
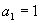 ,
,
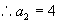 .
.
令 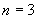 ,得
,得
 ,
,
 .令
.令 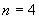 ,得
,得
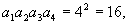
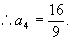
令 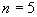 ,得
,得
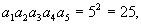
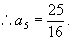
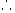
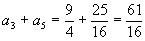 .
.
说明:本题涉及了方程的思想,同时体现了特殊与一般的关系.也可能有学生看出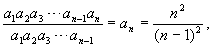 就求出了数列的通项公式,用代入法便可求出数列的任意一项,如果希望学生看出这一结果,可将所求换成求项数较大的项.
就求出了数列的通项公式,用代入法便可求出数列的任意一项,如果希望学生看出这一结果,可将所求换成求项数较大的项.
例3.数列 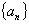 的通项公式为
的通项公式为
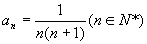 ,
,
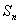 表示数列
表示数列
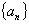 的前
的前
 项和,求
项和,求
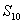 .
.
分析:数列的每一项
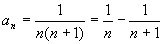 ,数列的前
,数列的前
 项和便抵消了一些项.
项和便抵消了一些项.
解: 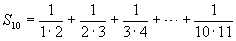


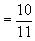 .
.
说明:可以在此补充裂项求和法,当然裂项法不仅仅针对分式形式的通项公式,只要
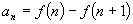 的形式就行.
的形式就行.
例4.在数列 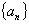 中,
中,
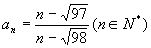 ,那么这个数列中的最大项与最小项的项数为____________.
,那么这个数列中的最大项与最小项的项数为____________.
分析:通过函数 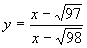 的取值情况来探求数列的最大项及最小项.
的取值情况来探求数列的最大项及最小项.
解:函数 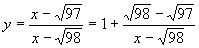 ,
,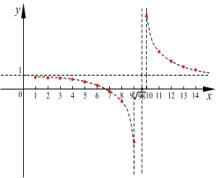 其图象是由函数
其图象是由函数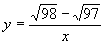 的图象向右平移
的图象向右平移
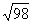 个单位,再向上平移1个单位得到,
个单位,再向上平移1个单位得到, 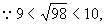 根据图象可得
根据图象可得
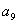 最小,
最小,
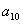 最大,即第9项最小,第10项最大.
最大,即第9项最小,第10项最大.
说明:数列的项与项数构成特殊的函数关系,研究其最值的方法就是求函数最值的基本方法,求函数最值的方法之一是数形结合,即利用函数图象来判断最值.
例5.设数列 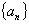 各项均为正数的数列,
各项均为正数的数列,
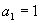 ,且满足:
,且满足:
 ,
,
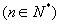 则数列
则数列
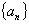 的通项公式为____________.
的通项公式为____________.
分析:解决此问题有两个思路,一是求出数列的前几项,由此猜出数列的通项公式(因为这是填空题);另一个思路是化简已知递推式(因式分解,降次),使
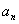 与
与
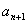 明确,简洁,便于寻求解决方式.
明确,简洁,便于寻求解决方式.
解:由已知得 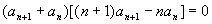 ,
,
 ,
,
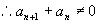 ,
,
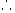
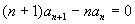 ,
, 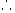
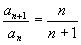 .
.
于是有  ,
,
这 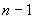 个等式相乘得
个等式相乘得
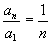 ,由于
,由于
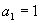 ,所以
,所以
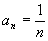 .
.
说明:这种方法叫做迭乘法,相类似的还有迭加法.
扩展资料

扩展资料
兔子繁殖问题与斐波那契
裴波那契(Fibonacci leonardo,约1170-1250)是意大利著名数学家. 他最重要的研究成果是在不定分析和数论方面,他的“裴波那契数列”成为世人们热衷研究的问题.
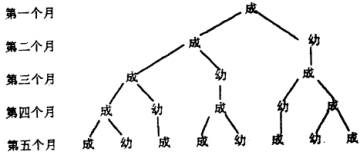 保存至今的裴波那契著作有5部,其中影响最大的是1202年在意大利出版的《算盘书》,《算盘书》中许多有趣的问题中最富成功的问题是著名的“兔子繁殖问题”. 如果每对兔子每月繁殖一对子兔,而子兔在出生后第二个月就有生殖能力,试问一对兔子一年能繁殖多少对兔子?可以这样思考:第一个月后即第二个月时,1对兔子变成了两对兔子,其中一对是它本身,另一对是它生下的幼兔. 第三个月时两对兔子变成了三对,其中一对是最初的一对,另一对是它刚生下来的幼兔,第三对是幼兔长成的大兔子.
第四个月时,三对兔子变成了五对,第五个月时,五对兔子变成了八对,这组数可以用图来表示,这组数从三个数开始,每个数是两个数的和,按此方法推算,第六个月是13对兔子,第七个月是21对兔子……,裴波那契得到一个数列,人们将这个数列前面加上一项1,成为“裴波那契数列”,即:1,1,2,3,5,8,13…. 数列用
保存至今的裴波那契著作有5部,其中影响最大的是1202年在意大利出版的《算盘书》,《算盘书》中许多有趣的问题中最富成功的问题是著名的“兔子繁殖问题”. 如果每对兔子每月繁殖一对子兔,而子兔在出生后第二个月就有生殖能力,试问一对兔子一年能繁殖多少对兔子?可以这样思考:第一个月后即第二个月时,1对兔子变成了两对兔子,其中一对是它本身,另一对是它生下的幼兔. 第三个月时两对兔子变成了三对,其中一对是最初的一对,另一对是它刚生下来的幼兔,第三对是幼兔长成的大兔子.
第四个月时,三对兔子变成了五对,第五个月时,五对兔子变成了八对,这组数可以用图来表示,这组数从三个数开始,每个数是两个数的和,按此方法推算,第六个月是13对兔子,第七个月是21对兔子……,裴波那契得到一个数列,人们将这个数列前面加上一项1,成为“裴波那契数列”,即:1,1,2,3,5,8,13…. 数列用 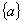 表示有:
表示有:
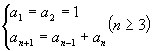 出人意料的是,这个数列在许多场合都会出现,在数学的许多不同分支中都能碰到它.
如果把普遍目前数列邻项之比作为一个新数列的项,我们得到:
出人意料的是,这个数列在许多场合都会出现,在数学的许多不同分支中都能碰到它.
如果把普遍目前数列邻项之比作为一个新数列的项,我们得到: 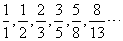 ,可以证明这个数列的极限是:
,可以证明这个数列的极限是:
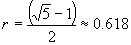 ,这是非常有名的黄金分割率,大自然中许多现象总是力求接近黄金比
,这是非常有名的黄金分割率,大自然中许多现象总是力求接近黄金比
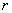 ,这个黄金比在科学中甚至艺术中也经常出现.
例如,宽比长的比等于黄金比
,这个黄金比在科学中甚至艺术中也经常出现.
例如,宽比长的比等于黄金比 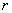 时最美:黄金比在古希腊建筑和陶瓷中可以经常见到埋在现代建筑设计等方面也越来越多地显示出黄金比的独特魅力.
裴波那契数列的许多有趣的性质和重要应用,引起了近800年数学历史上许多学者的兴趣,世界上有关裴波那契数列的研究文献多得惊人,裴波那契数列不仅是在初等数学中引人入胜,而且它的理论已广泛应用,特别是在数列、运筹学及优化理论方面为数学家们展开了一片施展才华的广阔空间.
时最美:黄金比在古希腊建筑和陶瓷中可以经常见到埋在现代建筑设计等方面也越来越多地显示出黄金比的独特魅力.
裴波那契数列的许多有趣的性质和重要应用,引起了近800年数学历史上许多学者的兴趣,世界上有关裴波那契数列的研究文献多得惊人,裴波那契数列不仅是在初等数学中引人入胜,而且它的理论已广泛应用,特别是在数列、运筹学及优化理论方面为数学家们展开了一片施展才华的广阔空间.
后人从裴波那契数列得到一系列的辉煌成果,但是我们不能忘记,这些成果都是起因与裴波那契的《算盘书》中提到的兔子问题.
探究活动
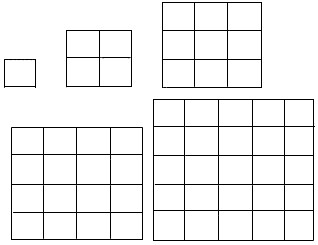
将边长为 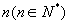 厘米的正方形分成
厘米的正方形分成
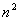 个边长为1厘米的正方形,数出其中所有正方形的个数.
个边长为1厘米的正方形,数出其中所有正方形的个数.
解:当 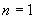 时,共有正方形
时,共有正方形
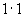 个;当
个;当
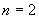 时,共有正方形
时,共有正方形
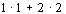 个;当
个;当
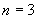 时,共有正方形
时,共有正方形
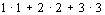 个;当
个;当
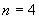 时,共有正方形
时,共有正方形
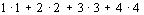 个;当
个;当
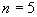 时,共有正方形
时,共有正方形
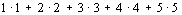 个;归纳猜想边长为
个;归纳猜想边长为
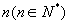 厘米的正方形中的正方形共有
厘米的正方形中的正方形共有
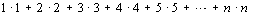 个.
个.
习题精选
(1)在数列 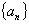 中,设
中,设
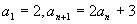 ,则通项
,则通项
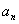 可能是( ).
可能是( ).
(A) 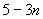 (B)
(B) 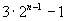
(C) 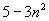 (D)
(D) 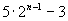
(2)已知数列 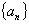 的通项公式是
的通项公式是
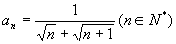 ,若
,若
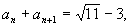 则
则
 的值为( ).
的值为( ).
(A)12 (B)9 (C) 8 (D) 6
(3)点 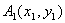 ,
,
 ,
,
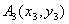 ,…,
,…,
 ,…是函数
,…是函数
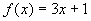 的图象上的一系列点,其中
的图象上的一系列点,其中
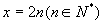 ,试写出数列
,试写出数列
 的前5项,并求出
的前5项,并求出 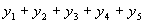 的值.
的值.
(4)已知数列 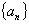 的前
的前
 项和
项和
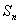 满足
满足
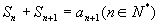 ,求证这个数列各项都等于同一个常数.
,求证这个数列各项都等于同一个常数.
2.数列的四种表示
1.数列的概念
3.(板书)数列的表示法
数列可看作特殊的函数,其表示也应与函数的表示法有联系,首先请学生回忆函数的表示法:列表法,图象法,解析式法.相对于列表法表示一个函数,数列有这样的表示法:用
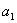 表示第一项,用
表示第一项,用
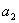 表示第一项,……,用
表示第一项,……,用
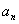 表示第
表示第
 项,依次写出成为
项,依次写出成为
(板书)(1)列举法
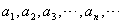 .(如幻灯片上的例子)简记为
.(如幻灯片上的例子)简记为
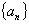 .
.
一个函数的直观形式是其图象,我们也可用图形表示一个数列,把它称作图示法.
(板书)(2)图示法
启发学生仿照函数图象的画法画数列的图形.具体方法是以项数
 为横坐标,相应的项
为横坐标,相应的项
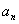 为纵坐标,即以
为纵坐标,即以
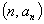 为坐标在平面直角坐标系中做出点(以前面提到的数列
为坐标在平面直角坐标系中做出点(以前面提到的数列
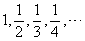 为例,做出一个数列的图象),所得的数列的图形是一群孤立的点,因为横坐标为正整数,所以这些点都在
为例,做出一个数列的图象),所得的数列的图形是一群孤立的点,因为横坐标为正整数,所以这些点都在
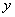 轴的右侧,而点的个数取决于数列的项数.从图象中可以直观地看到数列的项随项数由小到大变化而变化的趋势.
轴的右侧,而点的个数取决于数列的项数.从图象中可以直观地看到数列的项随项数由小到大变化而变化的趋势.
有些函数可以用解析式来表示,解析式反映了一个函数的函数值与自变量之间的数量关系,类似地有一些数列的项能用其项数的函数式表示出来,即
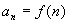 ,这个函数式叫做数列的通项公式.
,这个函数式叫做数列的通项公式.
(板书)(3)通项公式法
如数列  的通项公式为
的通项公式为
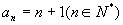 ;
;
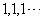 的通项公式为
的通项公式为
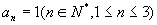 ;
;
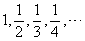 的通项公式为
的通项公式为 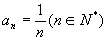 ;
;
数列的通项公式具有双重身份,它表示了数列的第
 项,又是这个数列中所有各项的一般表示.通项公式反映了一个数列项与项数的函数关系,给了数列的通项公式,这个数列便确定了,代入项数就可求出数列的每一项.
项,又是这个数列中所有各项的一般表示.通项公式反映了一个数列项与项数的函数关系,给了数列的通项公式,这个数列便确定了,代入项数就可求出数列的每一项.
例如,数列 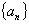 的通项公式
的通项公式
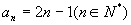 ,则
,则
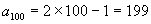 .
.
值得注意的是,正如一个函数未必能用解析式表示一样,不是所有的数列都有通项公式,即便有通项公式,通项公式也未必唯一.
除了以上三种表示法,某些数列相邻的两项(或几项)有关系,这个关系用一个公式来表示,叫做递推公式.
(板书)(4)递推公式法
如前面所举的钢管的例子,第
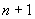 层钢管数
层钢管数
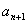 与第
与第
 层钢管数
层钢管数
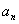 的关系是
的关系是
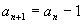 ,再给定
,再给定
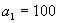 ,便可依次求出各项.再如数列
,便可依次求出各项.再如数列
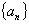 中,
中,
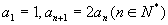 ,这个数列就是
,这个数列就是
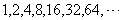 .
.
像这样,如果已知数列的第1项(或前几项),且任一项与它的前一项(或前几项)间的关系用一个公式来表示,这个公式叫做这个数列的递推公式.递推公式是数列所特有的表示法,它包含两个部分,一是递推关系,一是初始条件,二者缺一不可.
可由学生举例,以检验学生是否理解.
2.(板书)数列与函数的关系
数列可以看作特殊的函数,项数是其自变量,项是项数所对应的函数值,数列的定义域是正整数集
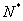 ,或是正整数集
,或是正整数集
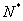 的有限子集
的有限子集
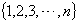 .
.
于是我们研究数列就可借用函数的研究方法,用函数的观点看待数列.
遇到数学概念不单要下定义,还要给其数学表示,以便研究与交流,下面探讨数列的表示法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com