
教学重点:以两角和的正弦、余弦和正切公式为基础,推导二倍角正弦、余弦和正切公式;
教学难点:二倍角的理解及其灵活运用.
以两角和正弦、余弦和正切公式为基础,推导二倍角正弦、余弦和正切公式,理解推导过程,掌握其应用.
(二)例题讲解
例1、已知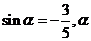 是第四象限角,求
是第四象限角,求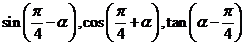 的值.
的值.
解:因为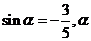 是第四象限角,得
是第四象限角,得 ,
,
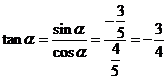 ,
,
于是有 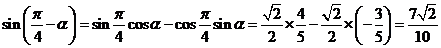
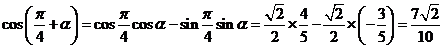
两结果一样,我们能否用第一章知识证明?
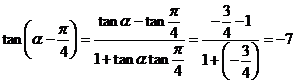
例2、利用和(差)角公式计算下列各式的值:
(1)、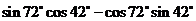 ;(2)、
;(2)、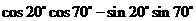 ;(3)、
;(3)、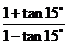 .
.
解:分析:解此类题首先要学会观察,看题目当中所给的式子与我们所学的两角和与差正弦、余弦和正切公式中哪个相象.
(1)、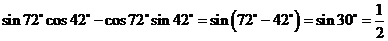 ;
;
(2)、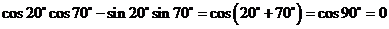 ;
;
(3)、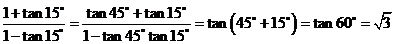 .
.
例3、化简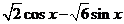
解:此题与我们所学的两角和与差正弦、余弦和正切公式不相象,但我们能否发现规律呢?
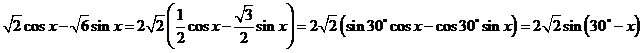 思考:
思考: 是怎么得到的?
是怎么得到的?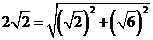 ,我们是构造一个叫使它的正、余弦分别等于
,我们是构造一个叫使它的正、余弦分别等于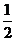 和
和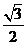 的.
的.
小结:本节我们学习了两角和与差正弦、余弦和正切公式,我们要熟记公式,在解题过程中要善于发现规律,学会灵活运用.
作业:
1、
已知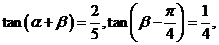 求
求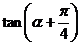 的值.(
的值.(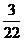 )
)
2、
已知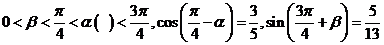 ,求
,求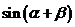 的值.
的值.
(胡仕伟)
§3.1.3 二倍角的正弦、余弦和正切公式
(一)复习式导入:大家首先回顾一下两角和与差的余弦公式:
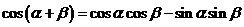 ;
;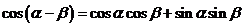 .
.
这是两角和与差的余弦公式,下面大家思考一下两角和与差的正弦公式是怎样的呢?
提示:在第一章我们用诱导公式五(或六)可以实现正弦、余弦的互化,这对我们解决今天的问题有帮助吗?
让学生动手完成两角和与差正弦和正切公式.
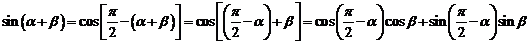
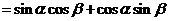 .
.
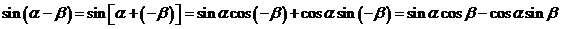 让学生观察认识两角和与差正弦公式的特征,并思考两角和与差正切公式.(学生动手)
让学生观察认识两角和与差正弦公式的特征,并思考两角和与差正切公式.(学生动手)
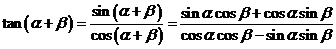 .
.
通过什么途径可以把上面的式子化成只含有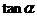 、
、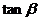 的形式呢?(分式分子、分母同时除以
的形式呢?(分式分子、分母同时除以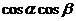 ,得到
,得到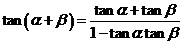 .
.
注意: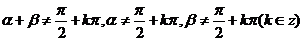
以上我们得到两角和的正切公式,我们能否推倒出两角差的正切公式呢?
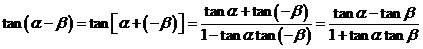
注意: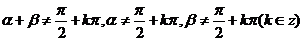 .
.
学法:研讨式教学
2. 教学难点:两角和与差正弦、余弦和正切公式的灵活运用.
1. 教学重点:两角和、差正弦和正切公式的推导过程及运用;
理解以两角差的余弦公式为基础,推导两角和、差正弦和正切公式的方法,体会三角恒等变换特点的过程,理解推导过程,掌握其应用.
(五)作业: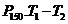
(胡仕伟)
§3.1.2 两角和与差的正弦、余弦、正切公式
(四)小结:本节我们学习了两角差的余弦公式,首先要认识公式结构的特征,了解公式的推导过程,熟知由此衍变的两角和的余弦公式.在解题过程中注意角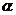 、
、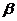 的象限,也就是符号问题,学会灵活运用.
的象限,也就是符号问题,学会灵活运用.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com