
3、对于两条直线a,b和平面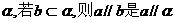 的
( )
的
( )
 A.充分但不必要条件 B.必要但不充分条件
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分也不必要条件
2、正项等比数列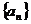 中,若
中,若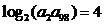 ,则
,则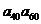 等于
( )
等于
( )
A. -16 B. 10 C. 16 D. 256
1、积分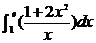 的值是
( )
的值是
( )
A. 1
 B. e
C. e+1 D.
e2
B. e
C. e+1 D.
e2
5. 三角恒等变换过程与方法,实际上是对三角函数式中的角、名、形的变换,即(1)找差异:角、名、形的差别;(2)建立联系:角的和差关系、倍半关系等,名、形之间可以用哪个公式联系起来;(3)变公式:在实际变换过程中,往往需要将公式加以变形后运用或逆用公式,如升、降幂公式, cosα= cosβcos(α-β)- sinβsin(α-β),1= sin2α+cos2α, =
=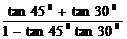 =tan(450+300)等。
=tan(450+300)等。
例题
例1 已知sin(α+β)=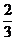 ,sin(α-β)=
,sin(α-β)=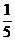 ,求
,求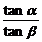 的值。
的值。
例2求值:cos24°﹣sin6°﹣cos72°
例3 化简(1)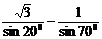 ;(2)sin2αsin2β+cos2αcos2β-
;(2)sin2αsin2β+cos2αcos2β-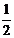 cos2αcos2β。
cos2αcos2β。
例4 设为锐角,且3sin2α+2sin2β=1,3sin2α-2sin2β=0,求证:α+2β=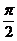 。
。
例5 如图所示,某村欲修建一横断面为等腰梯形的水渠,为降低成本,必须尽量减少水与水渠壁的接触面。若水渠断面面积设计为定值m,渠深8米。则水渠壁的倾角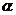 应为多少时,方能使修建的成本最低?
应为多少时,方能使修建的成本最低?
 分析:解答本题的关键是把实际问题转化成数学模型,作出横断面的图形,要减少水与水渠壁的接触面只要使水与水渠断面周长最小,利用三角形的边角关系将倾角为
分析:解答本题的关键是把实际问题转化成数学模型,作出横断面的图形,要减少水与水渠壁的接触面只要使水与水渠断面周长最小,利用三角形的边角关系将倾角为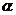 和横断面的周长L之间建立函数关系,求函数的最小值
和横断面的周长L之间建立函数关系,求函数的最小值
4.证明是利用恒等变换公式将等式的左边变同于右边,或右边变同于,或都将左右进行变换使其左右相等。
3.求值,要注意象限角的范围、三角函数值的符号之间联系与影响,较难的问题需要根据上三角函数值进一步缩小角的范围。
2.化简,要求使三角函数式成为最简:项数尽量少,名称尽量少,次数尽量底,分母尽量不含三角函数,根号内尽量不含三角函数,能求值的求出值来;
1.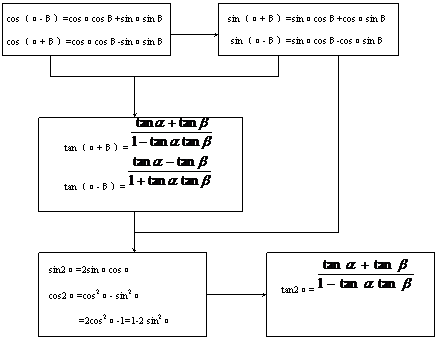 11个三角恒等变换公式中,余弦的差角公式是其它公式的基础,由它出发,用-β代替β、
11个三角恒等变换公式中,余弦的差角公式是其它公式的基础,由它出发,用-β代替β、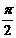 ±β代替β、α=β等换元法可以推导出其它公式。你能根据下图回顾推导过程吗?
±β代替β、α=β等换元法可以推导出其它公式。你能根据下图回顾推导过程吗?
进一步掌握三角恒等变换的方法,如何利用正、余弦、正切的和差公式与二倍角公式,对三角函数式进行化简、求值和证明:
学习和(差)公式,倍角公式以后,我们就有了进行变换的性工具,从而使三角变换的内容、思路和方法更加丰富,这为我们的推理、运算能力提供了新的平台.下面我们以习题课的形式讲解本节内容.
例1、试以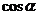 表示
表示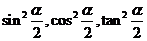 .
.
解:我们可以通过二倍角 和
和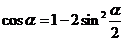 来做此题.
来做此题.
因为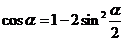 ,可以得到
,可以得到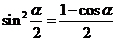 ;
;
因为 ,可以得到
,可以得到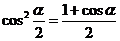 .
.
又因为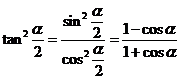 .
.
思考:代数式变换与三角变换有什么不同?
代数式变换往往着眼于式子结构形式的变换.对于三角变换,由于不同的三角函数式不仅会有结构形式方面的差异,而且还会有所包含的角,以及这些角的三角函数种类方面的差异,因此三角恒等变换常常首先寻找式子所包含的各个角之间的联系,这是三角式恒等变换的重要特点.
例2、求证:
(1)、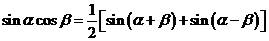 ;
;
(2)、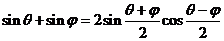 .
.
证明:(1)因为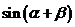 和
和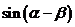 是我们所学习过的知识,因此我们从等式右边着手.
是我们所学习过的知识,因此我们从等式右边着手.
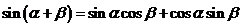 ;
;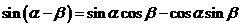 .
.
两式相加得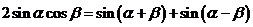 ;
;
即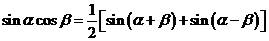 ;
;
(2)由(1)得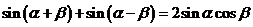 ①;设
①;设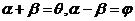 ,
,
那么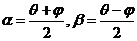 .
.
把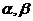 的值代入①式中得
的值代入①式中得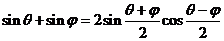 .
.
思考:在例2证明中用到哪些数学思想?
例2 证明中用到换元思想,(1)式是积化和差的形式,(2)式是和差化积的形式,在后面的练习当中还有六个关于积化和差、和差化积的公式.
例3、求函数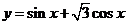 的周期,最大值和最小值.
的周期,最大值和最小值.
解: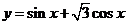 这种形式我们在前面见过,
这种形式我们在前面见过,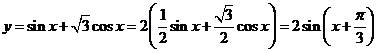 ,
,
所以,所求的周期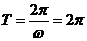 ,最大值为2,最小值为
,最大值为2,最小值为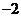 .
.
点评:例3是三角恒等变换在数学中应用的举例,它使三角函数中对函数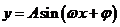 的性质研究得到延伸,体现了三角变换在化简三角函数式中的作用.
的性质研究得到延伸,体现了三角变换在化简三角函数式中的作用.
小结:此节虽只安排一到两个课时的时间,但也是非常重要的内容,我们要对变换过程中体现的换元、逆向使用公式等数学思想方法加深认识,学会灵活运用.
作业:
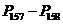
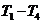
《三角恒等变换》复习课(2个课时)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com