11．(2007·汕头金山中学期末考试)已知圆C：x²+y²＝4和直线l：3x+4y+12＝0，点P是圆C上的一动点，直线与坐标轴的交点分别为点A、B.

(1)求与圆C相切且平行直线l的直线方程；

(2)求△PAB面积的最大值．

[解]　(1)设与圆C相切且平行直线l的直线方程为3x+4y+c＝0，则＝2，∴c＝±10.

所以，所求直线方程为3x+4y+10＝0或3x+4y－10＝0.

(2)不妨设直线l与x轴的交点为A，与y轴的交点为B，可求得A(－4,0)，B(0，－3)．

∴|AB|＝＝5.

圆C上的动点P到直线l的距离的最大值为两平行直线3x+4y+12＝0与3x+4y－10＝0间的距离．

即d＝＝，此时，△PAB面积取得最大值．S＝×|AB|·d＝×5×＝11.

10．设直线3x+4y+m＝0与圆x²+y²+x－2y＝0相交于P、Q两点，O为坐点原点，若OP⊥OQ，则m＝________.

[解析]　∵圆x²+y²+x－2y＝0过原点，并且OP⊥OQ，∴PQ是圆的直径，圆心的坐标为M(－，1)

又M(－，1)在直线3x+4y+m＝0上，

∴3×(－)+4×1+m＝0，　∴m＝－即为所求．

[答案]　－

9．若直线y＝x+k与曲线x＝恰有一个公共点，则k的取值范围是________．

[解析]　作y＝x+k与x＝的图象如图所示．

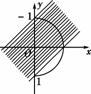
由图象可知有两种情况，相交与相切，

故－1<k≤1或k＝－.

∴k的取值范围为(－1,1]∪{－}．

[答案]　(－1,1]∪{－}

8．(2009·东莞二模)与圆x²+(y－2)²＝1相切，且在两坐标轴上截距相等的直线共有________条．

[答案]　4

7．(2009·广东高考，13)以点(2，－1)为圆心与直线x+y+6＝0相切的圆的方程________．

[答案]　(x－2)²+(y+1)²＝

6．(2008·湖北)过点A(11,2)作圆x²+y²+2x－4y－164＝0的弦，其中弦长为整数的共有

(　)

A．16条　 　　　　　 B．17条　 　　　　　 C．32条　 　　 D．34条

[解析]　∵点A(11,2)在圆C：(x+1)²+(y－2)²＝13²内，且|AC|＝12，∴过点A圆的最短的弦长l＝2＝10，∴10≤l≤26.而弦长最短和最长的直线仅有一条，故这样的直线有32条．

[答案]　C

5．(2008·安徽)若过点A(4,0)的直线l与曲线(x－2)²+y²＝1有公共点，则直线l的斜率的取值范围为

(　)

A．[－，]　 　　　　　　　　　　　 B．(－，)

C．[－，]　 　　　　　　　　　　　 D．(－，)

[解析]　点A(4,0)在圆外，因此斜率必存在．设经过该点的直线方程为kx－y－4k＝0，所以有≤1，解得≤k≤.从而选C.

[答案]　C

4．(2008·山东)已知圆的方程为x²+y²－6x－8y＝0.设该圆过点(3,5)的最长弦和最短弦分别为AC和BD，则四边形ABCD的面积为

(　)

A．10　 　　　　　 B．20　 　　　　　 C．30　 　　　　　 D．40

[解析]　∵圆方程为(x－3)²+(y－4)²＝25，∴|AC|＝2×5＝10.又点(3,5)到圆心距离d＝1，

∴|BD|＝2＝4.而AC⊥BD，

故四边形ABCD的面积为×10×4＝20.

[答案]　B

3．圆x²+y²－2x－5＝0与圆x²+y²+2x－4y－4＝0的交点为A，B，则线段AB的垂直平分线的方程是

(　)

A．x+y－1＝0　 　　　　　　　　　　　 B．2x－y+1＝0

C．x－2y+1＝0　 　　　　　　　　　　 D．x－y+1＝0

[解析]　线段AB的垂直平分线是过两圆圆心的直线．易求得两圆的圆心分别为C₁(1,0)，C₂(－1,2)，直线C₁C₂的方程为x+y－1＝0.故选A.

[答案]　A

2．过点(2,3)的直线l与圆C：x²+y²+4x+3＝0交于A、B两点，当弦长|AB|取最大值时，直线l的方程为

(　)

A．3x－4y+6＝0　 　　　　　　　　　 B．3x－4y－6＝0

C．4x－3y+8＝0　 　　　　　　　　　 D．4x+3y－8＝0

[解析]　∵过点(2,3)的圆中的最长弦AB必是圆的直径，由圆方程得圆心坐标为(－2,0)，∴直线AB的方程为y－3＝(x－2)，整理得3x－4y+6＝0，故应选A.

[答案]　A