
3.通过函数定义由变量观点向映射观点的过渡,是学生能从发展的角度看待数学的学习.
教学建议
2.通过函数概念的学习,使学生在符号表示,运算等方面的能力有所提高.
(1)对函数记号 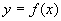 有正确的理解,准确把握其含义,了解
有正确的理解,准确把握其含义,了解
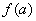 (
(  为常数)与
为常数)与 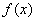 的区别与联系;
的区别与联系;
(2)在求函数定义域中注意运算的合理性与简洁性.
1.理解函数的概念,了解函数的三种表示法,会求函数的定义域.
(1)了解函数是特殊的映射,是非空数集A到非空数集B的映射.能理解函数是由定义域,值域,对应法则三要素构成的整体.
(2)能正确认识和使用函数的三种表示法:解析法,列表法,和图象法.了解每种方法的优点.
(3)能正确使用“区间”及相关符号,能正确求解各类函数的定义域.

扩展资料
逆映射
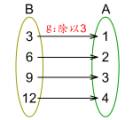
在本节中我们介绍了映射与一一映射的概念,并将以此为基础学习函数的概念.对于一一映射还可以进一步做一点研究.
如图:
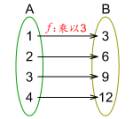
图(1) 图(2)
容易看出,图中(1)表示的映射是在 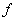 作用下,
作用下,
 到
到
 上的一一映射,图(2)所示的映射是在
上的一一映射,图(2)所示的映射是在 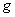 的作用下集合
的作用下集合
 到集合
到集合
 上的一一映射,在映射
上的一一映射,在映射
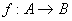 的作用下的象与原象,分别是在映射
的作用下的象与原象,分别是在映射
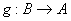 的作用下的原象与象,由此引出一个新概念称为逆映射.
的作用下的原象与象,由此引出一个新概念称为逆映射.
定义:设 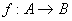 是集合
是集合
 到集合
到集合
 上的一一映射,如果对于
上的一一映射,如果对于
 中每一个元素
中每一个元素
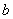 ,使
,使
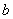 在
在
 中的原象
中的原象
 和它对应,这样得到的映射称为映射
和它对应,这样得到的映射称为映射
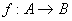 的逆映射,记作
的逆映射,记作
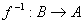 .
.
由定义不难看出只有一一映射才有逆映射,若
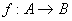 是一一映射,则
是一一映射,则
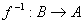 也是一一映射,刚才图中(1)(2),
也是一一映射,刚才图中(1)(2), 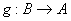 就是
就是
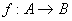 的逆映射.
的逆映射.
对于逆映射,它对于我们后面所学的反函数概念的理解有很大的帮助,也可以帮助我们认清反函数与原来函数之间的关系.
探究活动
(1) 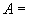 {整数},
{整数}, 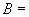 {偶数}, ,试问
{偶数}, ,试问  与
与
 中的元素个数哪个多?为什么?如果我们建立一个由
中的元素个数哪个多?为什么?如果我们建立一个由  到
到
 的映射对应法则
的映射对应法则
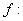 乘以2,那么这个映射是一一映射吗?
乘以2,那么这个映射是一一映射吗?
答案:两个集合中的元素一样多,它们之间可以形成一一映射.
(2)设 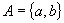 ,
,
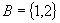 ,问最多可以建立多少种集合
,问最多可以建立多少种集合
 到集合
到集合
 的不同映射?若将集合
的不同映射?若将集合 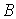 改为
改为
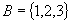 呢?结论是什么?如果将集合
呢?结论是什么?如果将集合  改为
改为
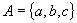 ,结论怎样?若集合
,结论怎样?若集合  改为
改为
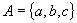 ,
,
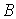 改为
改为
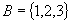 ,结论怎样?
,结论怎样?
从以上问题中,你能归纳出什么结论吗?依此结论,若集合A中含有 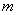 个元素,集合B中含有
个元素,集合B中含有 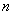 个元素,那么最多可以建立多少种集合
个元素,那么最多可以建立多少种集合
 到集合
到集合
 的不同映射?
的不同映射?
答案:若集合A含有m个元素,集合B含有n个元素,则不同的映射 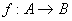 有
有
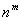 个.
个.
习题精选
(1)设集合 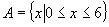 ,
,
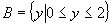 ,从
,从
 到
到
 的对应法则
的对应法则
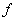 不是映射的是( ).
不是映射的是( ).
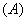
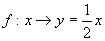
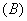
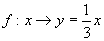
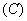
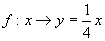
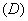
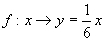
(2) 已知映射 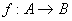 ,其中集合
,其中集合
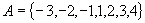 ,且对任意
,且对任意
 ,在
,在
 中和它对应的元素是
中和它对应的元素是
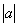 ,则集合
,则集合
 中元素的个数最少是___________.
中元素的个数最少是___________.
(3)设集合 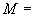
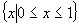 ,
,
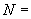
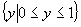 .下列四个图象中,表示从
.下列四个图象中,表示从
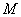 到
到
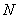 的映射的是( ).
的映射的是( ).
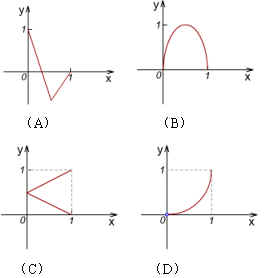
(4)已知从 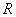 到
到
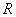 的映射
的映射
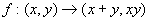 ,则
,则
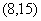 的原象是__________.
的原象是__________.
(5)已知从  到
到
 的映射是
的映射是
 ,从
,从
 到
到
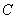 的映射是
的映射是
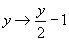 ,其中
,其中
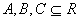 ,则从
,则从
 到
到
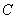 的映射是___________.
的映射是___________.
(6)已知集合 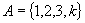 ,
,
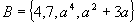 ,
,
且 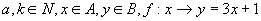 是由
是由
 到
到
 的一一映射,求
的一一映射,求
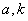 的值.
的值.
答案:(1)  ; (2) 4; (3)
; (2) 4; (3)
 ; (4)
; (4) 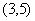 或
或
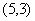 ; (5)
; (5) 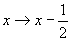 ; (6)
; (6) 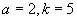
典型例题
例1 下列集合  到集合
到集合
 的对应中,判断哪些是
的对应中,判断哪些是
 到
到
 的映射? 判断哪些是
的映射? 判断哪些是  到
到
 的一一映射?
的一一映射?
(1) 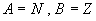 ,对应法则
,对应法则
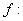
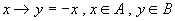 .
.
(2) 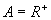 ,
,
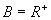 ,
,
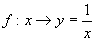 ,
,
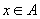 ,
,
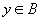 .
.
(3) 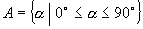 ,
,
 ,对应法则
,对应法则
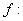 取正弦.
取正弦.
(4) 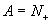 ,
,
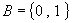 ,对应法则
,对应法则
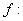 除以2得的余数.
除以2得的余数.
(5) 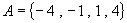 ,
,
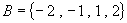 ,对应法则
,对应法则
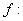
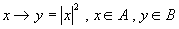 .
.
(6) 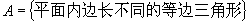 ,
,
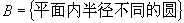 ,对应法则
,对应法则
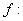 作等边三角形的内切圆.
作等边三角形的内切圆.
分析:解决的起点是读懂各对应中的法则含义,判断的依据是映射和一一映射的概念,要求对“任一对唯一”有准确的理解,对问题考虑要细致,周全.
解:(1)是映射,不是一一映射,因为集合  中有些元素(正整数)没有原象.
中有些元素(正整数)没有原象.
(2)是映射,是一一映射.不同的正实数有不同的唯一的倒数仍是正实数,任何一个正数都存在倒数.
(3)是映射,是一一映射,因为集合  中的角的正弦值各不相同,且集合
中的角的正弦值各不相同,且集合
 中每一个值都可以是集合
中每一个值都可以是集合
 中角的正弦值.
中角的正弦值.
(4)是映射,不是一一映射,因为集合  中不同元素对应集合
中不同元素对应集合
 中相同的元素.
中相同的元素.
(5)不是映射,因为集合  中的元素(如4)对应集合
中的元素(如4)对应集合  中两个元素(2和-2).
中两个元素(2和-2).
(6)是映射,是一一映射,因为任何一个等边三角形都存在唯一的内切圆,而任何一个圆都可以是一个等边三角形的内切圆.边长不同,圆的半径也不同.
说明:此题的主要目的在于明确映射构成的三要素的要求,特别是对于集合
 ,集合
,集合
 及对应法则
及对应法则
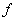 有哪些具体要求,包括对法则
有哪些具体要求,包括对法则
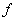 是数学符号语言给出时的理解.
是数学符号语言给出时的理解.
例2 给出下列关于从集合  到集合
到集合
 的映射的论述,其中正确的有_________.
的映射的论述,其中正确的有_________.
(1)  中任何一个元素在
中任何一个元素在
 中必有原象;
中必有原象;
(2)  中不同元素在
中不同元素在
 中的象也不同 ;
中的象也不同 ;
(3)  中任何一个元素在
中任何一个元素在
 中的象是唯一的;
中的象是唯一的;
(4)  中任何一个元素在
中任何一个元素在
 中可以有不同的象;
中可以有不同的象;
(5)  中某一元素在
中某一元素在
 中的原象可能不止一个;
中的原象可能不止一个;
(6)集合  与
与
 一定是数集;
一定是数集;
(7)记号 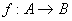 与
与
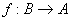 的含义是一样的.
的含义是一样的.
分析:此题是对抽象的映射概念的认识,理论性较强,要求较高,判断时可以让学生借助具体的例子来帮助.
解: (1)不对 (2)不对 (3)对 (4)不对 (5)对 (6)不对 (7)不对
说明:对此题的判断可以将映射中隐含的特点都描述出来,对映射的认识更加全面,准确.
例3 (1) 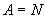 ,
, 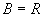 ,
,
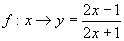 ,
,
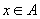 ,
,
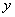
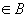 .在
.在
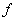 的作用下,
的作用下,
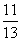 的原象是多少?14的象是多少?
的原象是多少?14的象是多少?
(2)设集合 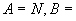 {偶数},映射
{偶数},映射 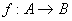 把集合A中的元素
把集合A中的元素  映射到集合B中的元素
映射到集合B中的元素 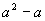 ,则在映射
,则在映射
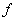 下,象20的原象是多少?
下,象20的原象是多少?
(3) 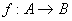 是从
是从
 到
到
 的映射,其中
的映射,其中
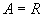 ,
,
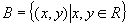 ,
,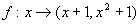 ,则
,则
 中元素
中元素
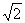 的象是多少?
的象是多少?  中元素
中元素
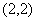 的原象是多少?
的原象是多少?
分析:通过此题让学生不仅会求指定元素象与原象,而且明确求象与原象的方法.
解:(1)由 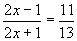 ,解得
,解得
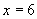 ,故
,故
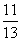 的原象是6;
的原象是6;
又 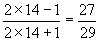 ,故14的象是
,故14的象是 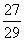 .
.
(2)由 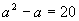 解得
解得
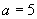 或
或
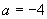 ,又
,又
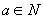 ,故
,故
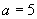 即20的原象是5.
即20的原象是5.
(3) 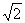 的象是
的象是
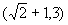 ,由
,由
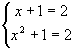 解得
解得
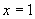 ,故
,故
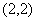 的原象是1.
的原象是1.
说明:此题主要作用在于明确利用代入法求指定元素的象,而求原象则需解方程或方程组.在本题中第(2)小题和第(3)小题在求象时,对  和
和
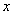 的制约条件都是两条,应解方程组,且还可以对方程组解的情况进行讨论(无解,有唯一解,无数解).其中第(3)小题集合
的制约条件都是两条,应解方程组,且还可以对方程组解的情况进行讨论(无解,有唯一解,无数解).其中第(3)小题集合
 中的元素应是二元数(有序数对),计算出的象必须写成有序数对的形式,所以求原象时必须先认清集合的特征.
中的元素应是二元数(有序数对),计算出的象必须写成有序数对的形式,所以求原象时必须先认清集合的特征.
2.2 函数
教学目标
2.一一映射是特殊的映射. 3.掌握求象与原象的方法.
1.映射是特殊的对应 
5.(板书)求象与原象.
例2 (1)从R到 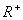 的映射
的映射
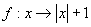 ,则R中的-1在
,则R中的-1在 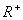 中的象是_____;
中的象是_____; 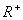 中的4在R中的原象是_____.
(2)在给定的映射
中的4在R中的原象是_____.
(2)在给定的映射 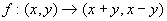 下,则点
下,则点
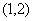 在
在
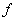 下的象是_____, 点
下的象是_____, 点
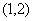 在
在
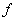 下的原象是______.
(3)
下的原象是______.
(3) 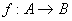 是集合A到集合B的映射,
是集合A到集合B的映射, 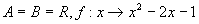 ,则A 中 元素
,则A 中 元素 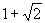 的象是_____,B中象0的原象是______, B中象-6的原象是______.
由学生先回答第(1)小题,之后让学生自己总结一下,应用什么方法求象和原象,学生找到方法后,再在方法的指导下求解另外两题,若出现问题,教师予以点评,最后小结求象用代入法,求原象用解方程或解方程组.
注意:所解的方程解的情况可能有多种如有唯一解,也可能无解,可能有无数解,这与映射的定义也是相吻合的.但如果是一一映射,则方程一定有唯一解.
的象是_____,B中象0的原象是______, B中象-6的原象是______.
由学生先回答第(1)小题,之后让学生自己总结一下,应用什么方法求象和原象,学生找到方法后,再在方法的指导下求解另外两题,若出现问题,教师予以点评,最后小结求象用代入法,求原象用解方程或解方程组.
注意:所解的方程解的情况可能有多种如有唯一解,也可能无解,可能有无数解,这与映射的定义也是相吻合的.但如果是一一映射,则方程一定有唯一解.
4.(板书)一一映射
(1)定义:设A,B是两个集合, 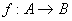 是集合A到集合B的映射,如果在这个映射下 对于集合A中的不同元素,在集合B中又不同的象,而且B中每一个元素都有原象,那么这个映射叫做A到B上的一一映射.
给出定义后,可再返回到刚才的例子,让学生比较它与映射的区别,从而进一步明确“一一”的含义.然后再安排一个例题.
例1 下列各表表示集合A(元素a)到集合B(元素b)的一个映射,判断这些映射是不是A到B上的一一映射.
是集合A到集合B的映射,如果在这个映射下 对于集合A中的不同元素,在集合B中又不同的象,而且B中每一个元素都有原象,那么这个映射叫做A到B上的一一映射.
给出定义后,可再返回到刚才的例子,让学生比较它与映射的区别,从而进一步明确“一一”的含义.然后再安排一个例题.
例1 下列各表表示集合A(元素a)到集合B(元素b)的一个映射,判断这些映射是不是A到B上的一一映射.
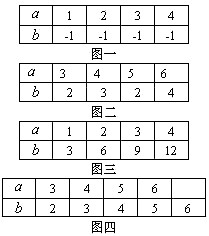
其中只有第三个表可以表示一一映射,由此例点明一一映射的特点 (板书)(2)特点:两个集合间元素是一对一的关系,不同的对的也一定是不同的(元素个数相同);集合B与象集C是相等的集合. 对于映射我们现在了解了它的定义及特殊的映射一一映射,除此之外对于映射还要求能求出指定元素的象与原象.
3.(板书)对概念的认识
(1) 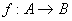 与
与
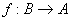 是不同的,即
是不同的,即
 与
与
 上有序的.
上有序的.
(2)象的集合是集合B的子集.
(3)集合A,B可以是数集,也可以是点集或其它集合.
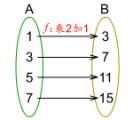
在刚才研究的基础上,教师再提出(2)和(4)有什么共性,能否把它描述出来,如果学生不能找出共性,教师可再给出几个例子,(用投影仪打出)
如:
(1) 
(2) 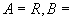 {数轴上的点},
{数轴上的点}, 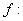 实数与数轴上相应的点对应.
(3)
实数与数轴上相应的点对应.
(3) 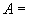 {中国,日本,韩国},
{中国,日本,韩国}, 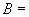 {北京,东京,汉城},
{北京,东京,汉城}, 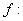 相应国家的首都.
引导学生在元素之间的对应关系和元素个数上找共性,由学生提出两点共性集合A中不同的元素对集合B中不同的元素;②B中所有元素都有原象.
那么满足以上条件的映射又是一种特殊的映射,称之为一一映射.
相应国家的首都.
引导学生在元素之间的对应关系和元素个数上找共性,由学生提出两点共性集合A中不同的元素对集合B中不同的元素;②B中所有元素都有原象.
那么满足以上条件的映射又是一种特殊的映射,称之为一一映射.
2.象与原象 可以用前面的例子具体说明谁是谁的象,谁是谁的原象. 提问3:下面请同学根据自己对映射的理解举几个映射的例子,看对映射是否真正认识了. (开始时只要是映射即可,之后可逐步提高要求,如集合是无限集,或生活中的例子等)由学生自己评判.之后教师再给出几个(主要是补充学生举例类型的不足)
(1) 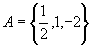 ,
,
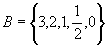 ,
,
 ,
,
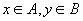 .
.
(2) 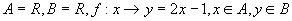 .
.
(3) 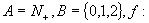 除以3的余数.
除以3的余数.
(4) 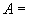 {高一1班同学},
{高一1班同学}, 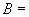 {入学是数学考试成绩},
{入学是数学考试成绩}, 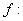 对自己的考试成绩.
对自己的考试成绩.
在学生作出判断之后,引导学生发现映射的性质(教师适当提出研究方向由学生说,再由老师概括)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com