
2.本质:函数是非空数集到非空数集的映射.(板书)
然后让学生试回答刚才关于
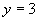 是不是函数的问题,要求从映射的角度解释.
是不是函数的问题,要求从映射的角度解释.
此时学生可以清楚的看到
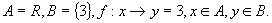 满足映射观点下的函数定义,故是一个函数,这样解释就很自然.
满足映射观点下的函数定义,故是一个函数,这样解释就很自然.
教师继续把问题引向深入,提出在映射的观点下如何解释
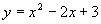 是个函数?
是个函数?
从映射角度看可以是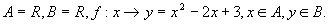 其中定义域是
其中定义域是
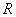 ,值域是
,值域是
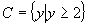 .
.
从刚才的分析可以看出,映射观点下的函数定义更具一般性,更能揭示函数的本质.这也是我们后面要对函数进行理论研究的一种需要.所以我们着重从映射角度再来认识函数.
1.定义:如果A,B都是非空的数集,那么A到B的映射 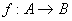 就叫做A到B的函数,记作
就叫做A到B的函数,记作 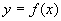 .其中原象集合A称为定义域,象集C
.其中原象集合A称为定义域,象集C 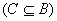 称为值域.
称为值域.
问题3:映射与函数有何关系?(函数一定是映射吗?映射一定是函数吗?)
引导学生发现,函数是特殊的映射,特殊在集合A,B必是非空的数集.
今天我们研究的内容是函数的概念.函数并不象前面学习的集合,映射一样我们一无所知,而是比较熟悉,所以我先找同学说说对函数的认识,如函数是什么?学过什么函数?
(要求学生尽量用自己的话描述初中函数的定义,并试举出各类学过的函数例子)
学生举出如 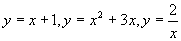 等,待学生说完定义后教师打出投影片,给出定义之后教师也举一个例子,问学生.
等,待学生说完定义后教师打出投影片,给出定义之后教师也举一个例子,问学生.
提问1. 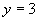 是函数吗?
是函数吗?
(由学生讨论,发表各自的意见,有的认为它不是函数,理由是没有两个变量,也有的认为是函数,理由是可以可做 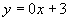 .)
.)
教师由此指出我们争论的焦点,其实就是函数定义的不完善的地方,这也正是我们今天研究函数定义的必要性,新的定义将在与原定义不相违背的基础上从更高的观点,将它完善与深化.
3.通过函数定义由变量观点向映射观点得过渡,使学生能从发展与联系的角度看待数学学习.
教学重点难点:重点是在映射的基础上理解函数的概念;
难点是对函数抽象符号的认识与使用.
教学用具:投影仪
教学方法:自学研究与启发讨论式.
教学过程:
2.通过对函数抽象符号的认识与使用,使学生在符号表示方面的能力得以提高.
1.理解函数的概念,了解函数三要素.
2.2 函数
教学目标:
2.教法建议
(1)高中对函数内容的学习是初中函数内容的深化和延伸.深化首先体现在函数的定义更具一般性.故教学中可以让学生举出自己熟悉的函数例子,并用变量观点加以解释,教师再给出如:
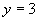 是不是函数的问题,用变量定义解释显得很勉强,而如果从集合与映射的观点来解释就十分自然,所以有重新认识函数的必要.
是不是函数的问题,用变量定义解释显得很勉强,而如果从集合与映射的观点来解释就十分自然,所以有重新认识函数的必要.
(2)对函数是三要素构成的整体的认识,一方面可以通过对符号 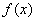 的了解与使用来强化,另一方面也可通过判断两个函数是否相同来配合.在这类题目中,可以进一步体现出三要素整体的作用.
的了解与使用来强化,另一方面也可通过判断两个函数是否相同来配合.在这类题目中,可以进一步体现出三要素整体的作用.
(3)关于对分段函数的认识,首先它的出现是一种需要,可以给出一些实际的例子来说明这一点,对自变量不同取值,用不同的解析式表示同一个函数关系,所以是一个函数而不是几个函数,其次还可以举一些数学的例子如
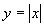 这样的函数,若利用绝对值的定义它就可以写成
这样的函数,若利用绝对值的定义它就可以写成
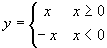 ,这就是一个分段函数,从这个题中也可以看出分段函数是一个函数.
,这就是一个分段函数,从这个题中也可以看出分段函数是一个函数.
教学设计方案
1.教材分析
(1)知识结构
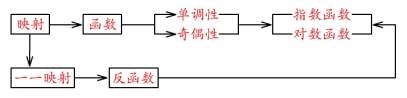
(2)重点难点分析
本小节的重点是在映射的基础上理解函数的概念.,主要包括对函数的定义,表示法,三要素的作用的理解与认识.教学难点是函数的定义和函数符号的认识与使用.
①由于学生在初中已学习了函数的变量观点下的定义,并具体研究了几类最简单的函数,对函数并不陌生,所以在高中重新定义函数时,重要的是让学生认识到它的优越性,它从根本上揭示了函数的本质,由定义域,值域,对应法则三要素构成的整体,让学生能主动将函数与函数解析式区分开来.对这一点的认识对于后面函数的性质的研究都有很大的帮助.
②在本节中首次引入了抽象的函数符号
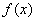 ,学生往往只接受具体的函数解析式,而不能接受
,学生往往只接受具体的函数解析式,而不能接受
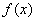 ,所以应让学生从符号的含义认识开始,在符号中,
,所以应让学生从符号的含义认识开始,在符号中,
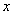 在法则
在法则
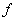 下对应
下对应
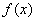 ,不是
,不是
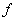 与
与
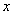 的乘积,符号本身就是三要素的体现.由于
的乘积,符号本身就是三要素的体现.由于
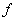 所代表的对应法则不一定能用解析式表示,故函数表示的方法除了解析法以外,还有列表法和图象法.此外
所代表的对应法则不一定能用解析式表示,故函数表示的方法除了解析法以外,还有列表法和图象法.此外
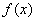 本身还指明了谁是谁的函数,有利于我们分清函数解析式中的常量与变量.如
本身还指明了谁是谁的函数,有利于我们分清函数解析式中的常量与变量.如
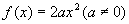 ,它应表示以
,它应表示以
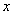 为自变量的二次函数,而如果写成
为自变量的二次函数,而如果写成
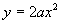 ,则我们就不能准确了解谁是变量,谁是常量,当
,则我们就不能准确了解谁是变量,谁是常量,当
 为变量时,它就不代表二次函数.
为变量时,它就不代表二次函数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com