
1、在平面内取定一点O,O点叫作极点:从O起引一条射线O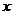 ,这条从极点起的射线O
,这条从极点起的射线O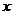 叫作极轴;选定长度单位,再选定角度的下方向(逆时针转角为正向),这种取定了极点、极轴、长度单位与角度正向的坐标系叫作极坐标系。建立极坐标系的要素是:极点、极径、长度单位、角度单位和它的正方向
叫作极轴;选定长度单位,再选定角度的下方向(逆时针转角为正向),这种取定了极点、极轴、长度单位与角度正向的坐标系叫作极坐标系。建立极坐标系的要素是:极点、极径、长度单位、角度单位和它的正方向
体会在极坐标系和平面直角坐标系中刻画点的位置的区别;体会在用方程刻画平面图形时选择适当坐标系的意义;通过阿基米德螺线,感受数学的文化价值。
教学重点:几类简单图形(过极点的直线、圆心在极点的圆、圆心有极轴,过极点的圆以及阿基米德螺线)的极坐标方程
教学难点:几类简单图形的极坐标方程的推导
教学过程
借助生活中的实例引入极坐标的概念;研究简单图形的极坐标方程的特点;比较简单图形在极坐标系和平面直角坐标系中的方程。
知道在极坐标系中刻画点的位置的方法;掌握简单图形(过极点的直线、圆心在极点的圆、圆心有极轴,过极点的圆以及阿基米德螺线)的极坐标方程
课本24页 习题2,4,
教学反思:
§1.3.2极坐标系
教学目标:
2、一般地,极坐标( ,
, )与(
)与( ,
,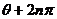 )表示同一个点,特别地,极点O的坐标为(0,
)表示同一个点,特别地,极点O的坐标为(0, )和直角坐标不同,平面内一个点的极坐标有无数种表示。
)和直角坐标不同,平面内一个点的极坐标有无数种表示。
1、要注意直角坐标与极坐标的区别,直角坐标系中平面上的点与有序数对(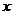 ,
,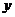 )是一一对应的,在极坐标系中,平面上的点与有序数对(
)是一一对应的,在极坐标系中,平面上的点与有序数对( ,
, )不是一一对应,只有在规定
)不是一一对应,只有在规定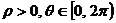 的前提下,并除极点外,点与极坐标之间才一一对应,在解题时要注意极坐标的多种表示形式。
的前提下,并除极点外,点与极坐标之间才一一对应,在解题时要注意极坐标的多种表示形式。
2、已知点A的极坐标(6, )分别写出给定条件下点A的极坐标
)分别写出给定条件下点A的极坐标
①若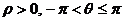 ;则A
;则A
②若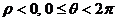 ,则A
,则A
③若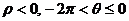 ,则A
,则A
1、已知两点的极坐标P(5,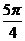 ),Q(1,
),Q(1,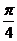 ),求线段PQ的长度
),求线段PQ的长度
例1、在极坐标系中,画出点A(1,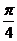 ),B(2,
),B(2,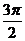 )C(3,
)C(3,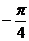 )D(4,
)D(4,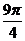 )
)
解析:在极坐标系中,先按极角找到极径所在的射线,即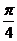 线,
线,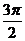 线,
线,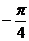 线,
线,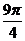 线,
线,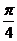 线和
线和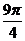 线是同一条射线,然后在相应的射线上按极径的数值描点。
线是同一条射线,然后在相应的射线上按极径的数值描点。
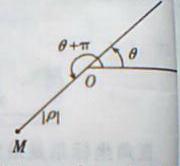 指出:我们也可以允许
指出:我们也可以允许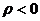 ,此时极坐标(
,此时极坐标( ,
, )对应的点M的位置按下面规则确定:点M在与极轴成
)对应的点M的位置按下面规则确定:点M在与极轴成 角的射线的反向延长线上,它到极为O的距离|
角的射线的反向延长线上,它到极为O的距离| |,即规定当
|,即规定当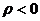 时,点M(
时,点M( ,
, )就是点M(
)就是点M( )
)
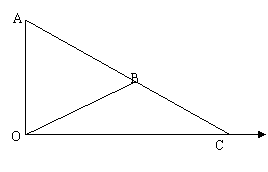
例2、如图在极坐标系中,写出点A,B,C,的极坐标,

解析:在极坐标系中,一般先按点与极点的距离求出极径的数值,然后按照极径所在的射线的位置求出极角。如图点A与极点O的距离为了,且在极轴上,所以A的极坐标为(1,0),同样可求得B,C的极坐标分别为(4,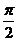 ),(5,
),(5,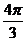 )
)
指出:已知点的位置求极坐标时,如果没有特殊要求,只要求一个解就可以了,由于点的极坐标的多值性,在需要写出通式的时候,求出一个解( ,
, )后,再写出其通式(
)后,再写出其通式( ,
,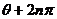 )或(
)或(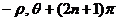 )
)
例3、已知点Q( ,
, ),分别按下列条件求出点P的极坐标。
),分别按下列条件求出点P的极坐标。
(1)M是点Q关于极点的对称点:(2)N是点Q关于直线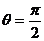 的对称点
的对称点
解:(1)由于M、Q关于极点对称得它们的极径OQ=OM,极角角相差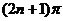 ,所以点M的极坐标为(
,所以点M的极坐标为( ,
,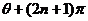 )或(
)或(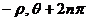 )(
)(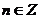 )
)
(2)由于点Q、N关于直线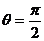 的对称,得它们的极径OQ=ON,点N的极角满足
的对称,得它们的极径OQ=ON,点N的极角满足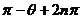 所以点N的极坐标为(
所以点N的极坐标为( ,
,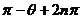 )
)
或(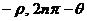 )(
)(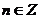 )
)
 例4、已知两点的极坐标A(3,
例4、已知两点的极坐标A(3,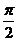 ),B(3,
),B(3,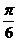 ),
),
求AB两点间的距离;AB与极轴正方向所成的角。
解法一:根据极坐标的定义,可得|OA|=|OB|=3,∠AOB=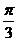 ,
,
即△AOB为等边三角形,所以|AB|=3,∠ACX=
法二:∵A 、B两点的极坐标分别为(3,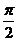 ),(3,
),(3,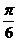 ),
),
∴|OA|=|OB|=3,∠AOC=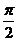 ,∠BOC=
,∠BOC=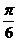 了 ∴∠AOB=
了 ∴∠AOB=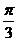 ,
,
在△AOB中,由余弦定理可得
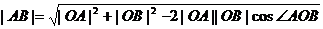
=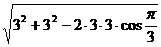 =3
=3
即△AOB为等边三角形,∠ACX=∠AOC+∠OAB=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com