
2、过已知点A(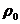 ,
,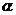 )且平行于极轴的直线的极坐标方程:
)且平行于极轴的直线的极坐标方程:
几类特殊曲线的极坐标方程
1、过极点直线的极坐标方程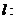

1、 设极点O到直线
设极点O到直线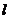 的距离为
的距离为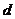 ,由点O向直线
,由点O向直线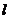 作垂线OA,由极轴到垂线OA的角度为
作垂线OA,由极轴到垂线OA的角度为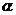 (如图所示)求已知直线
(如图所示)求已知直线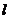 的极坐标方程
的极坐标方程
|
 和
和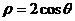 的位置关系
的位置关系例1、(1)求过点A(2,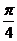 )且平行于极轴的直线的极坐标方程;
)且平行于极轴的直线的极坐标方程;
(2)过点A(3,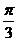 )且和极轴成
)且和极轴成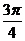 角的直线的极坐标方程
角的直线的极坐标方程
思路点拔:在已给极坐标系中,要想求直线的极坐标方程,就必须先寻找到几何等式。按照常规思路需构造关键三角形,利用关键三角形的边角关系引出几何意义。

 解法一:如图,在直线
解法一:如图,在直线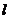 上任取一点M(
上任取一点M( ,
, )
)
在△OAM中
|OA|=2 |OM|=
|

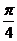 (或
(或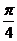 ) ∠OMA=
) ∠OMA= (或
(或
 )
)
在△OAM中由正弦定理得:
∴
解法二:如图在直线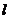 上任取一点M(
上任取一点M( ,
, )过M作MH⊥极轴于H点,
)过M作MH⊥极轴于H点,
 |MH|=2
|MH|=2 =
=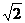
|
 即
即
(2)∠MBx=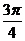 ,∠OAB=
,∠OAB=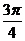
 =
=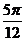
∴∠OMA=
在△MOA中,根据正弦定理
∴化简得直线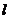 的极坐标方程为:
的极坐标方程为:
本题利用三角形法求出了直线方程,三角形法的步骤是:先根据题意作出(寻找)关键三角形,利用解三角形的知识列出几何等式,再将几何等式坐标化,化简、整理即得所求直线的极坐标方程。
例2、在极坐标系中,求以Q(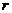 ,
,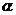 )为圆心,以
)为圆心,以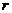 为半径的极坐标方程
为半径的极坐标方程
 解:由已知条件可知,此圆过极点。设点M(
解:由已知条件可知,此圆过极点。设点M( ,
, )为圆上任意一点,连结OQ交圆于点N,则ON为圆的直径,连结MN,则△OMN为直角三角形。
)为圆上任意一点,连结OQ交圆于点N,则ON为圆的直径,连结MN,则△OMN为直角三角形。
∠NOM=
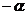 |ON|=2
|ON|=2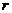
∴|OM|=|OM|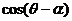 即
即 =2
=2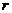
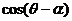
这就是所求的圆的极坐标方程。
4、阿基米德螺线
 一个动点M随时间的增加绕定点O逆(或顺)时针匀速绕动,同时离O点越来越远,它远离O点的直线距离也是匀速增长的,如果把O点定为极坐标的极点,M与O点的直线距离就是向径
一个动点M随时间的增加绕定点O逆(或顺)时针匀速绕动,同时离O点越来越远,它远离O点的直线距离也是匀速增长的,如果把O点定为极坐标的极点,M与O点的直线距离就是向径 ,转角就是极角
,转角就是极角 ,由于
,由于 与
与 的增加所用的时间是一致的,设开始时,动点在极点,则时间
的增加所用的时间是一致的,设开始时,动点在极点,则时间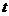 为
为 (
(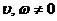 )
)
 一般地,将该式写成
一般地,将该式写成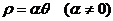
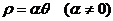 表示的曲线叫作阿基米德螺线,由于它向径的扩张与转角的变化皆为等速的,所以也称其为等速螺线。
表示的曲线叫作阿基米德螺线,由于它向径的扩张与转角的变化皆为等速的,所以也称其为等速螺线。
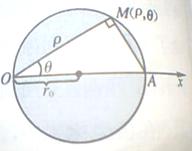
3、圆心在极轴,过极点的圆的极坐标方程
如图中画的是过极点,其中心在极轴的圆,设其半径为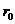
设此圆上任取一点M的极坐标为( ,
, ),由于OA是直径,所以∠OMA=
),由于OA是直径,所以∠OMA=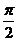 ,于是
,于是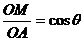 ,即
,即 从而得
从而得 与
与 满足的方程为:
满足的方程为: =2
=2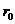
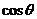
2、圆心在极点的圆的极坐标方程  =
=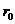
 方程
方程 =
=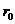 的含义是动点的极径恒为
的含义是动点的极径恒为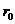 ,是个常数;而方程
,是个常数;而方程 =
=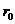 无极角
无极角 ,表示
,表示 可以任意变化,当极径
可以任意变化,当极径 是常数,极角任意时,即动保持与O点等距地转动,这正是圆规在画圆。
是常数,极角任意时,即动保持与O点等距地转动,这正是圆规在画圆。
在平面直角坐标系中,许多曲线的方程变得十分简洁,而且几何形象也表达得十分明确。所谓曲线L的极坐标方程是指L上的动点的极坐标的极径与极角满足的方程 或
或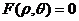
1、过极点直线的极坐标方程
在平面直角坐标系中,过原点O的直线方程形如: ,其中
,其中 是实数,叫作斜率,
是实数,叫作斜率,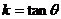 ,
, 是此直线与O
是此直线与O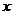 轴的夹角,这个角是多大,一般从
轴的夹角,这个角是多大,一般从 上不易看出来,需要计算
上不易看出来,需要计算 。但在极坐标中,我们取O
。但在极坐标中,我们取O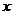 的正方向为极轴,则过极点O的射线方程写成
的正方向为极轴,则过极点O的射线方程写成 )
)
如果我们充许极径取负值,约定M ( ,
, )关于极点对称点N的极坐标写成N(
)关于极点对称点N的极坐标写成N( ),于是过原点与
),于是过原点与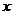 轴夹角为
轴夹角为 的直线的极坐标方程为
的直线的极坐标方程为
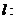

如与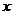 轴夹角为
轴夹角为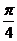 过原点的直线的极坐标方程为
过原点的直线的极坐标方程为 =
=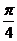
3、一般说来,由点求极坐标时,一般先按点与极点的距离求出极径的数值,并给出正号,然后按照它所在的直线的位置求出极角。
2、对于平面上的一个点M,连接极点O与M,线段OM之长 叫作M点的极径(或矢径、或向径),极轴O
叫作M点的极径(或矢径、或向径),极轴O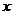 为始边按逆时针转到OM的角
为始边按逆时针转到OM的角 叫作M点的极角,有序数对(
叫作M点的极角,有序数对( ,
, )叫作M点的极坐标。当在建立了极坐标系的平面内给定一个点时,这个点的极坐标却不上唯一确定的,它可以有无数多种表示。
)叫作M点的极坐标。当在建立了极坐标系的平面内给定一个点时,这个点的极坐标却不上唯一确定的,它可以有无数多种表示。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com