
4.用稀碱性溶液或清水浸泡,可使残留在蔬菜上的农药降低毒性。如用碱性溶液浸泡蔬菜,可在水中加入适量的( )
A.纯碱 B.白酒 C.白糖 D.食醋
3.下列溶液酸性最强的是( )
A.pH=0的溶液 B. pH=1的溶液 C. pH=7的溶液 D. pH=14的溶液
2.用pH试纸测定某氢氧化钠溶液的酸碱度,如果先将蒸馏水润湿,再把白醋滴到试纸上,则测得的结果与原氢氧化钠溶液实际的pH比较( )
A.偏低 B.偏高 C.相等 D.无法比较
1.如果人体中的CO2不能顺利的排出体外,人体的血液pH将会( )
A.变大 B.变小 C.不变 D.先变大后变小
17. 抽象函数:抽象函数通常是指没有给出函数的具体的解析式,只给出了其它一些条件(如函数的定义域、单调性、奇偶性、解析递推式等)的函数问题。求解抽象函数问题的常用方法是:
(1)借鉴模型函数进行类比探究。几类常见的抽象函数 :
①正比例函数型: ---------------
--------------- ;
;
②幂函数型: --------------
-------------- ,
, ;
;
③指数函数型: ------------
------------ ,
, ;
;
④对数函数型: -----
----- ,
, ;
;
⑤三角函数型: -----
-----  。如已知
。如已知 是定义在R上的奇函数,且为周期函数,若它的最小正周期为T,则
是定义在R上的奇函数,且为周期函数,若它的最小正周期为T,则 ____(答:0)
____(答:0)
(2)利用函数的性质(如奇偶性、单调性、周期性、对称性等)进行演绎探究:如(1)设函数 表示
表示 除以3的余数,则对任意的
除以3的余数,则对任意的 ,都有 A、
,都有 A、 B、
B、 C、
C、 D、
D、 (答:A);(2)设
(答:A);(2)设 是定义在实数集R上的函数,且满足
是定义在实数集R上的函数,且满足 ,如果
,如果 ,
, ,求
,求 (答:1);(3)如设
(答:1);(3)如设 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,证明:直线
,证明:直线 是函数
是函数 图象的一条对称轴;(4)已知定义域为
图象的一条对称轴;(4)已知定义域为 的函数
的函数 满足
满足 ,且当
,且当 时,
时, 单调递增。如果
单调递增。如果 ,且
,且 ,则
,则 的值的符号是____(答:负数)
的值的符号是____(答:负数)
(3)利用一些方法(如赋值法(令 =0或1,求出
=0或1,求出 或
或 、令
、令 或
或 等)、递推法、反证法等)进行逻辑探究。如(1)若
等)、递推法、反证法等)进行逻辑探究。如(1)若 ,
, 满足
满足
 ,则
,则 的奇偶性是______(答:奇函数);(2)若
的奇偶性是______(答:奇函数);(2)若 ,
, 满足
满足
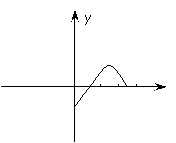
 ,则
,则 的奇偶性是______(答:偶函数);(3)已知
的奇偶性是______(答:偶函数);(3)已知 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, 的图像如右图所示,那么不等式
的图像如右图所示,那么不等式 的解集是_____________(答:
的解集是_____________(答: );(4)设
);(4)设 的定义域为
的定义域为 ,对任意
,对任意 ,都有
,都有 ,且
,且 时,
时, ,又
,又 ,①求证
,①求证 为减函数;②解不等式
为减函数;②解不等式 .(答:
.(答: ).
).
16. 函数的应用。(1)求解数学应用题的一般步骤:①审题――认真读题,确切理解题意,明确问题的实际背景,寻找各量之间的内存联系;②建模――通过抽象概括,将实际问题转化为相应的数学问题,别忘了注上符合实际意义的定义域;③解模――求解所得的数学问题;④回归――将所解得的数学结果,回归到实际问题中去。(2)常见的函数模型有:①建立一次函数或二次函数模型;②建立分段函数模型;③建立指数函数模型;④建立 型。
型。
15. 指数、对数值的大小比较:(1)化同底后利用函数的单调性;(2)作差或作商法;(3)利用中间量(0或1);(4)化同指数(或同真数)后利用图象比较。
14.指数式、对数式:
 ,
, ,,
,, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,  。如(1)
。如(1) 的值为________(答:8);(2)
的值为________(答:8);(2) 的值为________(答:
的值为________(答: )
)
13. 函数的周期性。
(1)类比“三角函数图像”得:
①若 图像有两条对称轴
图像有两条对称轴 ,则
,则 必是周期函数,且一周期为
必是周期函数,且一周期为 ;
;
②若 图像有两个对称中心
图像有两个对称中心 ,则
,则 是周期函数,且一周期为
是周期函数,且一周期为 ;
;
③如果函数 的图像有一个对称中心
的图像有一个对称中心 和一条对称轴
和一条对称轴 ,则函数
,则函数 必是周期函数,且一周期为
必是周期函数,且一周期为 ;
;
如已知定义在 上的函数
上的函数 是以2为周期的奇函数,则方程
是以2为周期的奇函数,则方程 在
在 上至少有__________个实数根(答:5)
上至少有__________个实数根(答:5)
(2)由周期函数的定义“函数 满足
满足
 ,则
,则 是周期为
是周期为 的周期函数”得:
的周期函数”得:
①函数 满足
满足 ,则
,则 是周期为2
是周期为2 的周期函数;
的周期函数;
②若 恒成立,则
恒成立,则 ;
;
③若 恒成立,则
恒成立,则 .
.
如(1) 设 是
是 上的奇函数,
上的奇函数, ,当
,当 时,
时, ,则
,则 等于_____(答:
等于_____(答: );(2)定义在
);(2)定义在 上的偶函数
上的偶函数 满足
满足 ,且在
,且在 上是减函数,若
上是减函数,若 是锐角三角形的两个内角,则
是锐角三角形的两个内角,则 的大小关系为_________(答:
的大小关系为_________(答: );(3)已知
);(3)已知 是偶函数,且
是偶函数,且 =993,
=993, =
= 是奇函数,求
是奇函数,求 的值(答:993);(4)设
的值(答:993);(4)设 是定义域为R的函数,且
是定义域为R的函数,且
 ,又
,又 ,则
,则 = (答:
= (答: )
)
12. 函数的对称性。
①满足条件 的函数的图象关于直线
的函数的图象关于直线 对称。如已知二次函数
对称。如已知二次函数 满足条件
满足条件 且方程
且方程 有等根,则
有等根,则 =_____(答:
=_____(答: );
);
②点 关于
关于 轴的对称点为
轴的对称点为 ;函数
;函数 关于
关于 轴的对称曲线方程为
轴的对称曲线方程为 ;
;
③点 关于
关于 轴的对称点为
轴的对称点为 ;函数
;函数 关于
关于 轴的对称曲线方程为
轴的对称曲线方程为 ;
;
④点 关于原点的对称点为
关于原点的对称点为 ;函数
;函数 关于原点的对称曲线方程为
关于原点的对称曲线方程为 ;
;
⑤点 关于直线
关于直线 的对称点为
的对称点为 ;曲线
;曲线 关于直线
关于直线 的对称曲线的方程为
的对称曲线的方程为 。特别地,点
。特别地,点 关于直线
关于直线 的对称点为
的对称点为 ;曲线
;曲线 关于直线
关于直线 的对称曲线的方程为
的对称曲线的方程为
 ;点
;点 关于直线
关于直线 的对称点为
的对称点为 ;曲线
;曲线 关于直线
关于直线 的对称曲线的方程为
的对称曲线的方程为 。如己知函数
。如己知函数 ,若
,若 的图像是
的图像是 ,它关于直线
,它关于直线 对称图像是
对称图像是 关于原点对称的图像为
关于原点对称的图像为 对应的函数解析式是___________(答:
对应的函数解析式是___________(答: );
);
⑥曲线 关于点
关于点 的对称曲线的方程为
的对称曲线的方程为 。如若函数
。如若函数 与
与 的图象关于点(-2,3)对称,则
的图象关于点(-2,3)对称,则 =______(答:
=______(答: )
)
⑦形如 的图像是双曲线,其两渐近线分别直线
的图像是双曲线,其两渐近线分别直线
(由分母为零确定)和直线 (由分子、分母中
(由分子、分母中 的系数确定),对称中心是点
的系数确定),对称中心是点 。如已知函数图象
。如已知函数图象 与
与 关于直线
关于直线 对称,且图象
对称,且图象 关于点(2,-3)对称,则a的值为______(答:2)
关于点(2,-3)对称,则a的值为______(答:2)
⑧ 的图象先保留
的图象先保留 原来在
原来在 轴上方的图象,作出
轴上方的图象,作出 轴下方的图象关于
轴下方的图象关于 轴的对称图形,然后擦去
轴的对称图形,然后擦去 轴下方的图象得到;
轴下方的图象得到; 的图象先保留
的图象先保留 在
在 轴右方的图象,擦去
轴右方的图象,擦去 轴左方的图象,然后作出
轴左方的图象,然后作出 轴右方的图象关于
轴右方的图象关于 轴的对称图形得到。
轴的对称图形得到。
如(1)作出函数 及
及 的图象;(2)若函数
的图象;(2)若函数 是定义在R上的奇函数,则函数
是定义在R上的奇函数,则函数 的图象关于____对称 (答:
的图象关于____对称 (答: 轴)
轴)
提醒:(1)从结论②③④⑤⑥可看出,求对称曲线方程的问题,实质上是利用代入法转化为求点的对称问题;(2)证明函数图像的对称性,即证明图像上任一点关于对称中心(对称轴)的对称点仍在图像上;(3)证明图像 与
与 的对称性,需证两方面:①证明
的对称性,需证两方面:①证明 上任意点关于对称中心(对称轴)的对称点仍在
上任意点关于对称中心(对称轴)的对称点仍在 上;②证明
上;②证明 上任意点关于对称中心(对称轴)的对称点仍在
上任意点关于对称中心(对称轴)的对称点仍在 上。如(1)已知函数
上。如(1)已知函数 。求证:函数
。求证:函数 的图像关于点
的图像关于点 成中心对称图形;(2)设曲线C的方程是
成中心对称图形;(2)设曲线C的方程是 ,将C沿
,将C沿 轴,
轴,  轴正方向分别平行移动
轴正方向分别平行移动 单位长度后得曲线
单位长度后得曲线 。①写出曲线
。①写出曲线 的方程(答:
的方程(答: );②证明曲线C与
);②证明曲线C与 关于点
关于点 对称。
对称。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com