5．温度：宏观上温度表示物体的冷热程度，微观上温度是物体大量分子热运动平均动能的标志．热力学温度和摄氏温度的数量关系：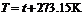

4．分子间的相互作用力：分子间同时存在着相互作用的引力和斥力，实际表现出来的分子力是引力和斥力的合力．分子间的斥力f_斥和引力f_引都随分子间距离r的增大而减小，但f_斥比f_引减小得更快．

3．分子永不停息地做无规则热运动的实验事实：扩散现象和布朗运动．

(1)扩散现象：不同物质能够彼此进入对方的现象．温度越高，扩散越快．

(2)布朗运动：悬浮在液体中微粒的无规则运动，微粒越小，温度越高，布朗运动越明显；

注意--各个方向液体分子对微粒冲力的不平衡性和无规则性引起布朗运动，布朗运动不是分子的运动，它间接地反映了液体分子的运动是永不停息的、无规则的．

(3)热运动：分子的无规则运动与温度有关，简称热运动，温度越高，这种运动越激烈．

2．物质是由大量分子组成的，分子体积极小(一般分子直径的数量级是10^-10m)

(1)实验：用油膜法估测分子大小--实验采用使油酸在水面上形成一层单分子油膜的方法估测分子的大小．可算出油酸分子的大小．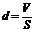

(2)1mol的任何物质含有的微粒数相同，其值为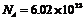mol^-1，称为阿伏加德罗常数．

(3)对微观量的估算

①分子的两种模型：球形或立方体模型

②利用阿伏加德罗常数是联系微观量与宏观量的桥梁作用进行估算．

1．分子动理论三个基本观点：物质是由大量分子组成的；分子永不停息地做无规则运动；分子之间存在着相互作用力(斥力和引力)．

10.

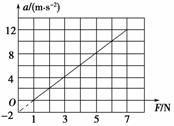
图3－1－16

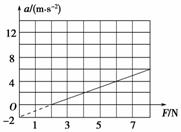
用水平力拉动物体在水平面上做加速直线运动．当改变拉力的大小时，物体运动的加速度也随之变化，a和F的关系如图3－1－16所示．g取10 m/s².

(1)根据图线所给的信息，求物体的质量及物体与水平面间的动摩擦因数；

(2)若改用质量是原来2倍的同种材料的物体，请在图3－1－16的坐标系上画出这种情况下的a－F图线．(要求写出作图的根据)

解析：(1)根据牛顿第二定律：F－μmg＝ma，所以a＝F－μg

可见a－F图象为一条直线，直线的斜率k＝＝2.0 kg^－1，纵轴截距为－μg＝－2.0 m/s²，

解得：物体的质量m＝0.50 kg，物体与地面间的动摩擦因数μ＝0.20.(也可以用横轴截距求动摩擦因数：当F＝1.0 N时，物体的加速度为零，物体所受阻力F_f＝F＝1.0 N，由F_f＝μmg解得物体与水平面间的动摩擦因数μ＝＝0.20.用其他方法结果正确也可)

(2)当物体质量加倍时，物体的加速度a＝F－μg

直线斜率k′＝＝1.0 kg^－1，纵轴的截距不变，作出如图所示的图线．

答案：(1)0.50 kg　0.20

(2)图见解析

9.

图3－1－15

(2009·安徽，22)在2008年北京残奥会开幕式上运动员手拉绳索向上攀登，最终点燃了主火炬，体现了残疾运动员坚韧不拔的意志和自强不息的精神．为了探求上升过程中运动员与绳索和吊椅间的作用，可将过程简化．一根不可伸缩的轻绳跨过轻质的定滑轮，一端挂一吊椅，另一端被坐在吊椅上的运动员拉住，如图3－1－15所示．设运动员的质量为65 kg，吊椅的质量为15 kg，不计定滑轮与绳子间的摩擦，重力加速度取g＝10 m/s².当运动员与吊椅一起正以加速度a＝1 m/s²上升时，试求：

(1)运动员竖直向下拉绳的力；

(2)运动员对吊椅的压力．

解析：解法一：设运动员和吊椅的质量分别为M和m，绳拉运动员的力为F.以运动员和吊椅整体为研究对象，受到重力的大小为(M+m)g，向上的拉力为2F，根据牛顿第二定律

2F－(M+m)g＝(M+m)a，F＝440 N，根据牛顿第三定律，运动员拉绳的力大小为440 N，方向竖直向下．

(2)以运动员为研究对象，运动员受到三个力的作用，重力大小Mg，绳的拉力F，吊椅对运动员的支持力F_N.根据牛顿第二定律：F+F_N－Mg＝Ma，F_N＝275 N，根据牛顿第三定律，运动员对吊椅的压力大小为275 N，方向竖直向下．

解法二：设运动员和吊椅的质量分别为M和m；运动员竖直向下对绳的拉力大小为F，对吊椅的竖直向下压力大小为F_N.根据牛顿第三定律，绳对运动员的拉力大小为F，吊椅对运动员的支持力大小为F_N.分别以运动员和吊椅为研究对象，根据牛顿第二定律：

F+F_N－Mg＝Ma①

F－F_N－mg＝ma②

由①②解得F＝440 N，F_N＝275 N

答案：(1)440 N，竖直向下　(2)275 N，竖直向下

8.

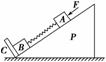
图3－1－14

如图3－1－14所示，在倾角为θ的光滑物块P的斜面上有两个用轻弹簧相连接的物体A和B；C为一垂直固定斜面的挡板，A、B质量均为m，弹簧的劲度系数为k，系统静止在水平面上．现对物体A施加一平行于斜面向下的力F压缩弹簧后，突然撤去外力F，则在物体B刚要离开C时(此过程中A始终没有离开斜面)(　)

A．物体B加速度大小为gsin θ　 　　　　B．弹簧的形变量为mgsin θ/k

C．弹簧对B的弹力大小为mgsin θ　 　 D．物体A的加速度大小为gsin θ

解析：当物体B刚要离开挡板C时，对物体B受力分析可得：kx－mgsin θ＝0，则选项A错误，BC正确；对物体A由牛顿第二定律可得：kx+mgsin θ＝ma_A，解得a_A＝2gsin θ，选项D错误．

答案：BC

7.

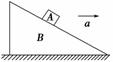
图3－1－13

如图3－1－13所示，物体A与斜面B保持相对静止并一起沿水平面向右做匀加速运动，当加速度a增大时，下列说法可能正确的是(　)

A．B对A的弹力不变，B对A的摩擦力可能减小

B．B对A的弹力增大，B对A的摩擦力大小可能不变

C．B对A的弹力增大，B对A的摩擦力一定增大

D．B对A的弹力增大，B对A的摩擦力可能减小

解析：本题考查牛顿第二定律的应用．物体和斜面保持相对静止，沿水平方向加速运动，则合力沿水平方向，竖直方向的合力为零，设斜面的倾角为θ，若开始静摩擦力的方向沿斜面向下，则F_Nsin θ+F_fcos θ＝ma，F_Ncos θ＝F_fsin θ+mg.若N增大，则F_f增大，因此此时，a增大，F_N、F_f都在增大．同理，若开始时静摩擦力方向沿斜面向上，则F_Nsin θ－F_fcos θ＝ma，F_Ncos θ+F_fsin θ＝mg，若F_N逐渐增大，则F_f沿斜面向上先逐渐减小到零，再沿斜面向下逐渐增大，此时B对A的弹力增大，B对A的摩擦力大小可能减小，可能为零，可能不变，可能增大，因此B、D项正确．

答案：BD

6.

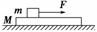
图3－1－12

如图3－1－12所示，质量为m的木块在质量为M的长木板上向右滑行，木块受到向右的拉力F的作用，长木板处于静止状态，已知木块与长木板间的动摩擦因数为μ₁，长木板与地面间的动摩擦因数为μ₂，则(　)

A．长木板受到地面的摩擦力的大小一定是μ₁mg

B．长木板受到地面的摩擦力的大小一定是μ₂(m+M)g

C．当F>μ₂(m+M)g时，长木板便会开始运动

D．无论怎样改变F的大小，长木板都不可能运动

解析：木块受到的滑动摩擦力大小为μ₁mg，由牛顿第三定律，长木板受到m对它的摩擦力大小也是μ₁mg，对长木板使用平衡条件得地面对长木板的静摩擦力为μ₂mg，A正确．改变F的大小，木块m受到的滑动摩擦力不会发生变化，长木板受力不变，D正确．

答案：AD