21.(07福建•理•18题)如图，正三棱柱的所有棱长都为2，D为中点。

(Ⅰ)求证：AB₁⊥面A₁BD；(Ⅱ)求二面角的大小；

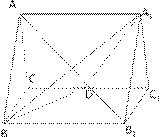
20.如图，在长方体AC₁中，AD=AA₁=1，AB=2，点E在棱AB上移动.(1)证明：D₁E⊥A₁D；

(3)　　　　　　　　　　　 当E为AB的中点时，求点E到面ACD₁的距离；(3)AE等于何值时，二面角D₁-EC-D的大小为.

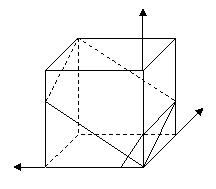
19.(07江苏)如图，已知是棱长为的正方体，点在上，点在上，且．

(1)求证：四点共面；(4分)；(2)若点在上，，点在上，，垂足为，求证：平面；(4分)；(3)用表示截面和侧面所成的锐二面角的大小，求．

18.如图，在五面体中，点是矩形的对角线的交点，面是等边三角形，棱．

(1)　　　　　　　　　　　 证明//平面；

(2)　　　　　　　　　　　 设，证明平面．

17.(2008北京卷16)如图，在三棱锥中，，

，．

　 (Ⅰ)求证：；(Ⅱ)求二面角的大小；(Ⅲ)求点到平面的距离．

16、等边三角形与正方形有一公共边，二面角的余弦值为，分别是的中点，则所成角的余弦值等于　　　　　

15、如图，正方体中，M、N、P、Q、R、S分别是AB、BC、、、、的中点，则下列判断：(1)PQ与RS共面；(2)MN与RS共面；(3)PQ与MN共面；则正确的结论是＿＿＿＿＿

14、已知、是两个不同的平面，m、n是平面及平面之外的两条不同直线，给出四个论断：①m∥n，②∥，③m⊥，④n⊥，以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题：＿＿＿＿

13、一个正方体的各定点均在同一球的球面上，若该球的体积为，则该正方体的表面积为　　　　　　　　　　 .

12、某几何体的一条棱长为，在该几何体的正视图中，这条棱的投影是长为的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别是长为a和b的线段，则a+b的最大值为(　　 )A.　B.　C.　D.