例1　已知A(3,2)，B(-4,1)，C(0,-1)。求直线AB，BC，CA的斜率，并判断这些直线的倾斜角是钝角还是锐角。

师生活动预设：

学生易通过斜率公式计算出结果，再由斜率的符号断定直线的倾斜角的性质。教师再引导学生通过画图象观察验证。

设计意图:

本题的重点是让学生体会通过代数的运算可以研究几何图形的性质。

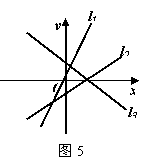
变式1:如图5，直线l₁，l₂，l₃的斜率分别为k₁，k₂，k₃，则下列不等式成立的是(　 )

A. k₁>k₂ >k₃　 B. k₂>k₁ >k₃　

C. k₃>k₂ >k₁ D. k₃>k₁ >k₂

变式2:已知过原点的直线l₁，l₂，l₃的斜率分别为2，1，-1。试在直角坐标系中画出这三条直线。

设计意图:

考查学生对直线倾斜角概念的理解以及对倾斜角和斜率、直线上两点坐标与斜率之间关系的认识，通过做题，使学生进一步体会数与形之间的相互联系与转化。

问题3:两点确定一直线，你能根据直线上两点的坐标求直线的倾斜角和斜率吗?

(1)如图3，若已知点A(1,3)，B(3,1)，C(6,7)，D(3,7)，试求直线AB，BC，CD，DA的斜率和倾斜角。

　 (图3)

(2)如图4，若已知点P₁(x₁,y₁)，P₂(x₂,y₂)，求直线P₁P₂的斜率。

　　　　 (图4)　　　　　

师生活动预设：

学生有了三角和平几的知识，有能力进行自主探究。对所得的结论，教师可以追问:

(1)如果直线P₁P₂平行于x轴，或与x轴重合时，上述结论还适用吗?为什么?

(2)如果直线P₁P₂平行于y轴，或与y轴重合时，上述结论还适用吗?为什么?

(3)如果某倾斜角为60°的直线l上有任意两点A(a₁,a₂)，B(b₁,b₂)，式子是定值吗?为什么?

设计意图:

从特殊到一般，顺势推导出斜率公式，通过公式进一步体会“比值”的含义，并使学生经历通过坐标的代数运算研究直线的几何性质的过程。体会倾斜角与斜率的内在联系，初步感受斜率在沟通数与形上的作用。

21．仔细观察下面这幅漫画，然后回答问题。(4分)

(1)简要介绍漫画的内容(3分)

(2)给这幅漫画拟写一个标题(不超过4个字)(1分)

20．下面一段话划线的部分在表述上有多处语病，请找出来任意三处并加以修改。(6分)

最高人民法院有关负责人介绍，①行政诉讼法施行以来，②人民法院依法审理、受理了大量行政案件，有效地化解了行政争议，维护了人民群众的合法权益，促进了行政机关依法行政，③行政审判的特殊职能作用日益彰显。但是，④最高人民法院开通的民意沟通信箱征集的意见来看，行政诉讼“告状难”现象依然存在。最高人民法院为此进行了深入调研，⑤并在此基础上出台了《关于保护行政诉讼当事人诉权的意见》，⑥其目的是为了督促各级人民法院进一步重视和加强行政案件受理，依法保护当事人诉讼权利，⑦切实解决行政诉讼“告状难”。

15．填空。 (6分)

(1)联想是思维的一种形式。王勃在《　　　 》中的名句“　　　　　　　　　　 ，秋水共长天一色”是由空间接近引起的联想；“故垒西边，　人道是，　　　　　　 　　　　”是由历史事件发生地点的相关引起的联想；“问君能有几多愁，　　　　　　　　　 　”是由特征相似引起的联想。

(2)《　　　　　 》是我国第一部国别体史书，相传为左丘明所著。

(3)　　　　　　　　 被称为19世纪俄国最伟大的作家，著有里程碑式巨著《安娜·卡列尼娜》。