(一)改变条件：

例4、在例3中，若将直线MN向上平移至与圆O相交时，m、n、p之间又有什么关系？

　　　 分析：过O点作OC垂直于EF，垂足为C，

　　　　　 ，所以

　　　　　 因为则

，可得

(二)条件与结论互换：

例5、在梯形ABCD中，AD∥BC，∠C=90⁰，且AD+BC=AB，

求证：(1)CD与以AB为直径的圆相切；

(2)AB与以CD为直径的圆相切。

分析：紧密联系两个基本图形，利用逆向思维，根据

圆的切线的判断定理准备条件可以得证。

运用(一)：直接运用研究成果

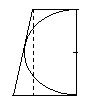例1、在梯形ABCD中，AD∥BC，∠BCD=90⁰，以CD为直径的半圆O切AB于点E，这个梯形的面积为21CM² ，周长为20 CM ，求半圆O的半径长

分析：(1)从已知条件出发：

　　 (2)从未知条件出发：求半径r

(3)找等量关系，列方程组解得或

(4)结论取舍：过点A作AF⊥BC，垂足为F，AB>AF，即必须满足AD+BC>2r，所以求得r=3cm。

运用(二)：从复杂图形中分解出基本图形

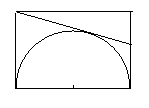例2、在矩形ABCD中，以AB为直径作半圆O，E是BC的中点，若DE是半圆O的切线，切点为F，试求的值。

　　　 分析：四边形ABED是直角梯形，满足基本图形1，

利用研究结论可以求解；或利用圆的切线长

定理转化到中利用勾股定理可求的值。

运用(三)：联系基本图形，代数与几何知识的综合运用

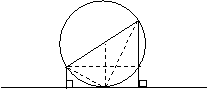例3、如图，已知直线MN和⊙O切于点C，AB是⊙O的直径，AE⊥MN，BF⊥MN，垂足分别为E、F，设AE=m，EF=p，BF=n

(1)求证：p²=4mn

(2)求证：EC、FC的长是方程的两个根

　　　 分析：利用基本图形2，连接OC、AC、BC，

　　　　　　 可利用∽证明；也可以过

　　　　　　 点A作，在中利用勾股定理证明。

不仅从相同的“圆与直角梯形”中找出不同点：

条件不同点：基本图形1是以垂直于底边的腰为直径作圆；基本图形2则是以不垂直于底边的腰为直径作圆

结论不同点：基本图形1中圆与两底相切，但基本图形2不成立；基本图形2中圆心与切点的连线是梯形的中位线，但基本图形1不成立

又可以从不同的基本图形中找出相同之处：

特征相同点：圆与直角梯形，都是以一腰为直径且与另一腰相切

结论相同点：两个基本图形都有AB=AD+BC成立

通过对两个基本图形进行对比研究，加强对基本图形特征的记忆和理解。

(四)过点A作AF⊥BC，垂足为F：(10)AB²=AF²+BF²(其中AB=AD+BC，BF=BC-AD)

　　 当然，在这两个基本图形中又隐含了多个其它基本图形，一旦发现就可以实现基本图形间的整合和转化。

(三)连结OD、OE：(9)OE垂直平分线段DC(即OD=OC)

(二)连结AE、BE：(6)∠AEB=90⁰(7)△ADE∽△ECB

(8)DE²=AD·BC

(五)过点A作AF⊥BC，垂足为F：(12)AB²=AF²+BF² (其中AF=DC，BF=BC-AD)

　　 在整个研究过程中，完全任由学生的思维发散。让学生通过研究，发现一个看似简单的图形原来可以得出这么多的结论。没有发现的同学也会不自觉地接受了其他同学分析问题的方法和常见辅助线作法。如此以来，学生再一次看到满足此特征的基本图形就立刻能够得到以上相关结论。

　 　基本图形2：以直角梯形不垂直于底边的腰为直径作圆与另一腰相切。是将基本图形1稍作变动，学生经过探究同基本图形1一样可以得出四类结论。

(一)连结OE：(1)OE⊥DC(2)OE∥AD∥BC(3)DE=EC(4)OE是梯形ABCD的中位线，即OE=(AD+BC)(5)AB=2EO=AD+BE

(四)连结DE、CE：(11)DE⊥EC(∠DEC=90⁰)

(三)(连结OA、OB：(5)Rt△ADO≌Rt△AEO(6)Rt△BEO≌Rt△BCO(7)∠1=∠2，∠3=∠4(8)∠2+∠3=90⁰(AO⊥BO)(9)Rt△ADO∽Rt△OCB(10)OD²=AD·BC

(二)连结OE：(4)OE⊥AB(∠OEA=90⁰)