
5.函数y=f(x)的图象在点P(1,f(1))处的切线方程为y=-2x+10,
 导函数为
导函数为 ,则f(1)+
,则f(1)+ 的值为
的值为 
A. -2 B.2 C
.6 D.
8
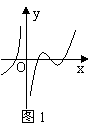
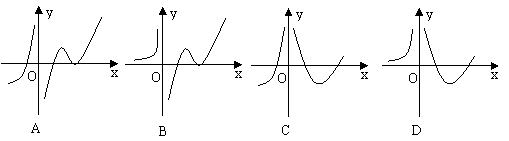 6设函数f(x)在定义域内可导,y=f(x)的图象如图1所示,则导函数y=f ¢(x)可能为
6设函数f(x)在定义域内可导,y=f(x)的图象如图1所示,则导函数y=f ¢(x)可能为





4.若一系列函数的解析式相同,值域也相同,但定义域不同,则称这些函数为“同族函数”,那么解析式为 ,值域为{1,4}的“同族函数”共有
,值域为{1,4}的“同族函数”共有
A.4个
B.8个
C.9个 D.16个
3.若函数f(x)= (
( )在区间[2,+¥
)在区间[2,+¥ 上递增,则实数
上递增,则实数 的范围是
的范围是
A.(-¥,4 B.(-4,4
B.(-4,4

C. -4,2)
D.(-¥,-4)∪[2,+¥
-4,2)
D.(-¥,-4)∪[2,+¥

2.集合 ,集合
,集合 ,则P与Q的关系是
,则P与Q的关系是 
A.P=Q B.P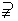 Q
C.P
Q
C.P Q D.P∩Q=Æ
Q D.P∩Q=Æ
1.设集合 等于
等于
A.{1,2,3} B.{0,1,2,3} 
C.{2} D.{-1,0,1,2,3}
17、(本小题满分13分)已知向量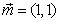 ,向量
,向量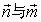 的夹角为
的夹角为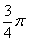 ,且
,且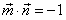 。
。
(1)求向量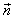 ;
;
(2)设向量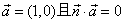 ,向量
,向量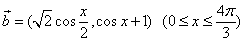 ,试求
,试求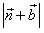 的取值范围。
的取值范围。
18(本小题满分13分)已知数列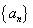 的前
的前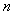 项和为
项和为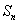 ,若
,若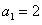 ,且
,且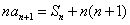 。
。
(1)求数列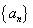 的通项公式;
的通项公式;
(2)令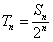 ,①当n为何正整数时,
,①当n为何正整数时,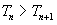 ;②若对一切正整数n总有
;②若对一切正整数n总有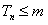 求实数
求实数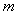 的取值范围。
的取值范围。
19(本小题满分13分)商场销售某种商品,售出件数是商品标价的一次函数,标价越高,售出件数越少。当标价为18元时,售出件数为0。已知该商品成本价为8元/件,商场以高于成本价格(标价)出售。
(1)商场要获得最大利润,该商品的标价应定为每件多少元?
(2)通常情况下,获得最大利润只是一种“理想结果”,如果商场希望其利润不小于“理想结果”的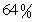 ,那么其标价必须不低于多少元/件?
,那么其标价必须不低于多少元/件?
20(本小题满分14分)设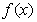 是定义在
是定义在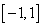 上的偶函数,
上的偶函数,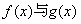 图像关于直线
图像关于直线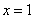 对称,且当
对称,且当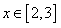 时,
时,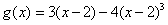 。
。
(1)求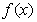 的表达式;
的表达式;
(2)若不等式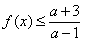 对一切
对一切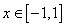 都成立,求实数
都成立,求实数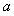 的取值范围。
的取值范围。
21(本小题满分14分)设函数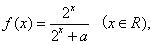 且满足
且满足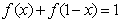 。
。
(1)求实数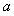 的值;
的值;
(2)若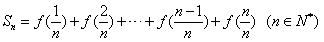 ,求
,求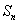 表达式;
表达式;
(3)记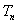 为数列
为数列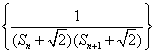 的前项和,若
的前项和,若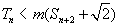 对一切
对一切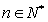 都成立,求实数
都成立,求实数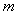 的取值范围。
的取值范围。
“华安、连城、永安、漳平一中,龙海二中,泉港一中”六校联考
16、(本小题满分13分)已知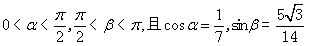 。
。
求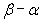 的值。
的值。
15、若数列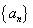 满足
满足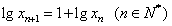 ,且
,且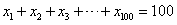 ,
,
则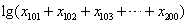 的值为 。
的值为 。
14、已知关于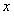 的不等式
的不等式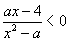 的解集为M,若
的解集为M,若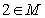 且
且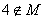 ,则实数
,则实数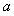 的取值范围为 ;
的取值范围为 ;
13、已知函数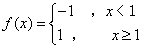 , 则不等式
, 则不等式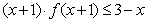 的解集为 ;
的解集为 ;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com