
16.(本小题满分12分)
设角A,B,C为△ABC的三个内角.
(Ⅰ)若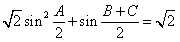 ,求角A的大小;
,求角A的大小;
(Ⅱ)设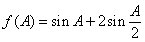 ,求当A为何值时,f(A)取极大值,并求其极大值.
,求当A为何值时,f(A)取极大值,并求其极大值.
[解析](Ⅰ)由已知,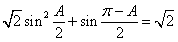 ,即
,即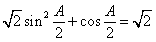 . (2分)
. (2分)
所以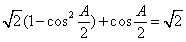 ,即
,即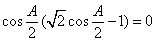 .
(4分)
.
(4分)
在△ABC中,因为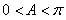 ,则
,则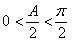 ,所以
,所以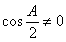 ,从而
,从而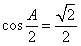 . (5分)
. (5分)
而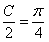 ,即
,即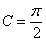 .
(6分)
.
(6分)
(Ⅱ)因为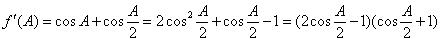 . (8分)
. (8分)
因为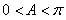 ,则
,则 .由
.由 ,得
,得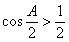 ,所以
,所以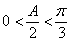 ,即
,即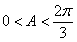 .、
.、
所以当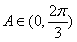 时,
时,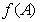 为增函数;当
为增函数;当 时,
时,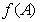 为减函数.
(10分)
为减函数.
(10分)
故当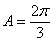 时,
时,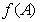 取极大值,且极大值为
取极大值,且极大值为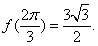 (12分)
(12分)
15.设a,b,λ都为正数,且a≠b,对于函数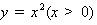 图象上两点
图象上两点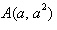 ,
,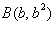 .
.
(1)若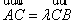 ,则点C的坐标是
,则点C的坐标是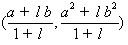 ;
;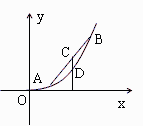
(2)过点C作x轴的垂线,交函数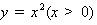 的图象于D点,
的图象于D点,
由点C在点D的上方可得不等式: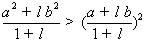 .
.
[解析](1)设点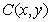 ,因为点
,因为点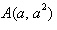 ,
,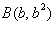 ,
,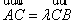 ,则
,则
 ,所以
,所以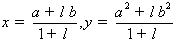 .
.
(2)因为点C在点D的上方,则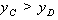 ,所以
,所以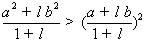 .
.
14.若函数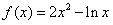 在其定义域内的一个子区间
在其定义域内的一个子区间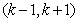 内不是单调函数,则实数k 的取值范围是
内不是单调函数,则实数k 的取值范围是 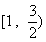 .
.
[解析]因为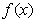 定义域为
定义域为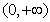 ,又
,又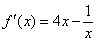 ,由
,由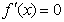 ,得
,得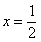 .
.
据题意,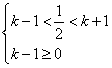 ,解得
,解得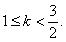
0.3×0.1×100=3.因为前四组的频数成等比数列,则 视力在4.6-4.7的频数为1×33=27.
视力在4.6-4.7的频数为1×33=27.
因为后6组的频数成等差数列,设公差为d,则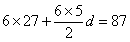 ,解得
,解得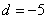 .
.
故视力在4.6-5.0之间的学生人数为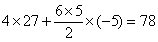 (人).
(人).
13.随机抽查某中学 高三年级100名学生的视力情况,得其频率分布直方图如下图所示.已知前4组的频数成等比数列,后6组的频数成等差数列,则视力在4.6到5.0之间的学生人数为 78 人.
高三年级100名学生的视力情况,得其频率分布直方图如下图所示.已知前4组的频数成等比数列,后6组的频数成等差数列,则视力在4.6到5.0之间的学生人数为 78 人.
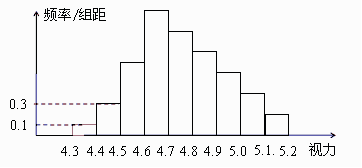
[解析]由直方图知,视力在4.3-4.4的频数为0.1×0.1×100=1,视力在4.4-4.5的频数 为
为
12.如图,A,B是两圆的交点,AC是小圆的直径,D和E分别是CA和CB的延长线与大圆的交点,已知AC=4,BE=10,且BC=AD ,则AB=
,则AB=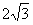 .
.
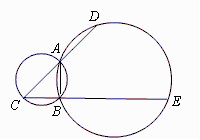
[解析]设 ,由割线定理,得CA×CD=CB×CE,即
,由割线定理,得CA×CD=CB×CE,即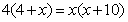 .
.
解得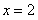 ,因为AC是小圆的直径,则
,因为AC是小圆的直径,则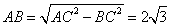 .
.
11.已知点A(1,2),直线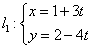 (t为参数)与直线
(t为参数)与直线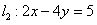 相交于点B,则A、B两点之间的距离|AB|=
相交于点B,则A、B两点之间的距离|AB|=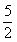 .
.
[解析]将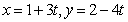 代入
代入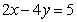 ,得
,得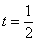 ,所以|
,所以| AB|=5t=
AB|=5t=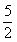 .
.
10.计算: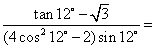 -4 .
-4 .
[解析]原式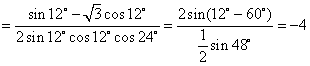 .
.
9.不等式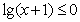 的解集是 (-1,0] .
的解集是 (-1,0] .
[解析]由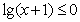 ,得
,得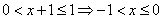 .
.
8.设 与
与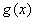 是定义在同一区间[a,b]上的两个函数,若对任意x∈[a,b],都有
是定义在同一区间[a,b]上的两个函数,若对任意x∈[a,b],都有
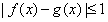 成立,则称
成立,则称 和
和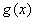 在[a,b]上是“密切函数”,区间[a,b]称为“密切区间”.若
在[a,b]上是“密切函数”,区间[a,b]称为“密切区间”.若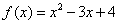 与
与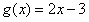 在[a,b]上是“密切函数”,则其“密切区间”可以是 ( D )
在[a,b]上是“密切函数”,则其“密切区间”可以是 ( D )
A. [1,4] B. [2,4] C. [3,4] D. [2,3]
[解析]因为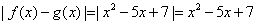 .由
.由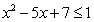 ,得
,得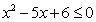 ,解得
,解得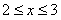 ,故选D.
,故选D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com