9．若≤x≤，则函数y＝的值域是________．

答案：[+1,4]

解析：＝tanx+1，≤x≤.

∴1≤tanx≤，∴y∈[+1,4]．

8．若0<x<，则下列命题中正确的是(　)

A．sinx<x　 　　　　　　　　　　　　　　　　　　　　 B．sinx>x

C．sinx<x2　 　　　　　　　　　　　　　　　　　　　 D．sinx>x2

答案：D

解法一：特殊值法：令x＝，sin＝，·x2＝排除选项A、B、C，故选D.

解法二：f(x)＝sinx－，f′(x)＝cosx－，

g(x)＝sinx－，g′(x)＝cosx－x，

当x∈时，∵f′(x)先正后负．∴f(x)先增后减．

f(0)＝0.f＝1－＝－<0.

∴f(x)在时不恒大于0，故不选A、B.

∵g′(x)在上是减函数g′(0)＝1>0，

g′＝－<0.g(0)＝0，g＝0.

∴g(x)在恒大于0，故选D.

7.

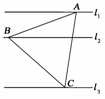
如右图，l₁、l₂、l₃是同一平面内的三条平行直线，l₁与l₂间的距离是1，l₂与l₃间的距离是2，正三角形ABC的三顶点分别在l₁、l₂、l₃上，则△ABC的边长是(　)

A．2　 　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　 D.

答案：D

解析：设其边长为a，AB与l2的夹角为θ，易知1＝asinθ，2＝asin(60°－θ)．于是cosθ－sinθ＝0.∴tanθ＝.cosθ＝＝，∴sinθ＝.∴a＝＝.故选D.

6．设两个向量a＝(λ+2，λ2－cos2α)和b＝，其中λ，m，α为实数．若a＝2b，则的取值范围是(　)

A．[－6,1]　　　　　　　　　　　　　　 B．[4,8]

C．(－∞，1]　 　　　　　　　　　　　　　　　　　　　 D．[－1,6]

答案：A

解析：∵2b＝(2m，m+2sinα)，∴λ+2＝2m，

λ2－cos2α＝m+2sinα，

∴(2m－2)2－m＝cos2α+2sinα，

即4m2－9m+4＝1－sin2α+2sinα，

又∵－2≤1－sin2α+2sinα≤2，

∴－2≤4m2－9m+4≤2，

解得≤m≤2，∴≤≤4，

又∵λ＝2m－2，∴＝2－，

∴－6≤2－≤1，故选A.

5．(2008·北京丰台)若f(x)＝2cos2x+sin2x+a(a为实常数)在区间上的最小值为－4，则a的值为(　)

A．4　 　　　　　　　　　　　　　　　　　　　　　　　　　 B．－3

C．－4　 　　　　　　　　　　　　　　　　　　　　　　　 D．－6

答案：C

解析：f(x)＝2cos2x+sin2x+a＝1+cos2x+sin2x+a＝1+a+2sin，

当kπ－≤x≤kπ+(k∈Z)时函数为增函数，当kπ+≤x≤kπ+(k∈Z)时函数为减函数，在区间上的最小值f＝1+a+2sin＝a＝－4，故选C.

4．(2009·江西五校4月)若对可导函数f(x)，g(x)，当x∈[0,1]时恒有f′(x)·g(x)<f(x)·g′(x)，若已知α、β是一锐角三角形的两个内角，且α≠β，记F(x)＝(g(x)≠0)，则下列不等式正确的是(　)

A．F(sinα)<F(cosβ)　 　　　　　　　　　　　　　　 B．F(sinα)>F(sinβ)

C．F(cosα)>F(cosβ)　 　　　　　　　　　　　　　　 D．F(cosα)<F(cosβ)

答案：A

解析：F(x)＝(g(x)≠0)，F′(x)＝<0，F(x)在[0,1]上为减函数，又α，β是一锐角三角形的两个内角，且α≠β，则α+β>，α>－β，sinα>cosβ，F(sinα)<F(cosβ)，故选A.

3．(2009·湖北八校联考二)已知函数f(x)＝sin(ωx+φ)(ω>0，x∈R)对定义域内的任意x，都满足条件f(x)＝f(x+1)－f(x+2)，若A＝sin(ωx+φ+9ω)，B＝sin(ωx+φ－9ω)，则有(　)

A．A>B　 　　　　　　　　　　　　　　　　　　　　　　　 B．A＝B

C．A≥B　 　　　　　　　　　　　　　　　　　　　　　　 D．A<B

答案：B

解析：函数f(x)＝sin(ωx+φ)(ω>0，x∈R)对定义域内的任意x，都满足条件f(x)＝f(x+1)－f(x+2)，也满足条件f(x+1)＝f(x+2)－f(x+3)，两式相加得f(x)＝－f(x+3)，周期为6，又A＝sin(ωx+φ+9ω)＝sin[ω(x+9)+φ]，B＝sin(ωx+φ－9ω)＝sin[ω(x－9)+φ]，它们相差3个周期，则有A＝B，故选B.

2．(2009·石家庄一模)设动直线x＝a与函数f(x)＝2sin2(+x)和g(x)＝cos2x的图象分别交于M、N两点，则|MN|的最大值为(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C．2　 　　　　　　　　　　　　　　　　　　　　　　　　　 D．3

答案：D

解析：f(x)－g(x)＝2sin2(+x)－cos2x＝1－cos2(+x)－cos2x＝1+2sin(2x－)∈[－1,3]，则|MN|的最大值为3，故选D.

1．(2009·福建质检)已知函数f(x)满足f(π+x)＝f(π－x)，且当x∈(0，π)时，f(x)＝x+cosx，则f(2)，f(3)，f(4)的大小关系是(　)

A．f(2)<f(3)<f(4)　　　　　　　　　　　　　　 B．f(2)<f(4)<f(3)

C．f(4)<f(3)<f(2)　 　　　　　　　　　　　　　　　　 D．f(3)<f(4)<f(2)

答案：B

解析：函数f(x)满足f(π+x)＝f(π－x)，则其对称轴为x＝π，当x∈(0，π)时，f(x)＝x+cosx，f′(x)＝1－sinx≥0，f(x)为增函数，则在(π，2π)上f(x)为减函数，3与π相距最近，其函数值最大，2与π相距最远，其函数值最小，则f(2)，f(3)，f(4)的大小关系是f(2)<f(4)<f(3)．

22.(本小题满分14分)已知a≥，f(x)=－a²x²+ax+c.

(1)证明对任意x∈［0，1］，f(x)≤1的充要条件是c≤;

(2)已知关于x的二次方程f(x)=0有两个实根α、β，证明：|α|≤1且|β|≤1的充要条件是c≤a²－a.