1.　　 从平衡的速率角度思考如何选择合成氨气的条件？

3.　　 用碳酸氢铵和食盐制备碳酸钠，了解氯碱工业的资料。

(教学内容增减建议)淡化合成氨的化学原理讲述，主要培养分析流程和装置图的能力，利用原料气的获得，强化反应方程式的书写；增加候氏制碱法的讲述。

(课时安排)第一单元用4课时；第二单元3课时，第三单元3课时。复习2课时。共12课时

第一单元　氨的合成以及候氏制碱法(4、5、6课时)

(知识回顾)

2.　　 了解合成氨的主要反应原理、原料、重要设备、流程和意义，认识催化剂的研制对促进化学工业发展的重大意义。

1.　　 了解我国主要生产资源、基本化工产品的主要种类和发展概况。

15．已知函数y＝Asin(ωx+φ)，x∈R，A>0，ω>0，|φ|<，若该函数图象上的一个最高点坐标为(，3)，与其相邻的对称中心的坐标是(－，0)．

(1)求函数y＝Asin(ωx+φ)的解析式；

(2)(理)求函数图象在x＝－处的切线方程．

(文)求函数的最小值，并写出函数取得最小值时自变量x的集合．

解：(1)由题意知A＝3，T＝－(－)＝，

所以T＝π，ω＝＝2.

y＝3sin(2x+φ)，又由2×+φ＝2kπ+，k∈Z，φ＝2kπ+，k∈Z，因为|φ|<，所以φ＝.

y＝3sin(2x+)，x∈R

(2)(理)y′＝6cos(2x+)，y′|x＝－＝3.

函数图象在x＝－处的切线方程为y+＝3(x+)，即3x－y－+π＝0.

(文)由(1)知，函数的最小值为－3；

由2x+＝2kπ－，k∈Z得x＝kπ－，k∈Z，

∴函数取得最小值时自变量x的集合为{x|x＝kπ－，k∈Z}．

14.

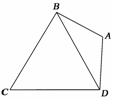
如右图，在平面四边形ABCD中，AB=AD=1，∠BAD=θ，而△BCD是正三角形．

(1)将四边形ABCD面积S表示为θ的函数；

(2)求S的最大值及此时θ角的值．

解：(1)△ABD的面积S₁＝×1×1×sinθ＝sinθ，

∵△BDC是正三角形，

则△BDC的面积S₂＝BD².

而在△ABD中由余弦定理可知：

BD₂＝12+12－2×1×1×cosθ＝2－2cosθ.

于是四边形ABCD面积S＝sinθ+(2－2cosθ)，

S＝+sin，其中0<θ<π.

(2)由S＝+sin及0<θ<π，

则－<θ－<.在θ－＝时，

S取得最大值1+.此时θ＝+＝.

13．(2008·江西·7)在△ABC中，a、b、c分别为角A、B、C所对的边长，a＝2，tan+tan＝4，sinBsinC＝cos2.求A、B及b、c.

解：由tan+tan＝4得

cot+tan＝4，化简得＝4，

所以sinC＝，又C∈(0，π)，

即C＝或C＝.

由sinBsinC＝cos2得

sinBsinC＝[1+cos(B+C)]，

即cos(B－C)＝1，

所以B＝C＝，A＝π－(B+C)＝.

由正弦定理＝＝得

b＝c＝a＝2×＝2.

12．已知函数f(x)＝sin(2x－)+2sin2(x－)(x∈R)．

(Ⅰ)求函数f(x)的最小正周期；

(Ⅱ)求使函数f(x)取得最大值时x的集合．

解：(Ⅰ)f(x)＝sin(2x－)+1－cos2(x－)

＝2[sin2(x－)－cos2(x－)]+1

＝2sin[2(x－)－]+1＝2sin(2x－)+1.

∴T＝＝π.

(Ⅱ)当f(x)取最大值时，sin(2x－)＝1，有

2x－＝2kπ+，即x＝kπ+　(k∈Z)，

∴所求x的集合为{x∈R|x＝kπ+，k∈Z}．

11．(2009·沈阳二测)给出下列命题：

①函数y＝sin|x|不是周期函数；

②函数y＝tanx在定义域内为增函数；

③函数y＝|cos2x+|的最小正周期为；

④函数y＝4sin(2x+)，x∈R的一个对称中心为(－，0)

其中正确命题的序号为________．

答案：①④

解析：对于①，函数y＝sin|x|不是周期函数，则①正确；对于②，函数y＝tanx在定义域内不是单调函数，则②不正确；对于③，函数y＝|cos2x+|不是周期函数，则③不正确；对于④，经验证函数y＝4sin(2x+)，x∈R的一个对称中心为(－，0)，则④正确；综上所述，应填①④.

10．(2008·湖北五市联考)若函数f(x)＝(1+cosx)10+(1－cosx)10，x∈[0，π]，则其最大值等于________．

答案：210(或1024)

解析：由二项式定理可得，f(x)＝(C010cos0x+C110cos1x+…+C1010cos10x)+(C010cos0x－C110cos1x+C210cos2x－…+C1010cos10x)＝2(C010cos0x+C210cos2x+…+C1010cos10x)，所以f(x)的最大值为2(C010+C210+…+C1010)＝210＝1024.