1．由于地球的自转，地球表面上各点均做匀速圆周运动，所以(　　 )

A．地球表面各处具有相同大小的线速度

B．地球表面各处具有相同大小的角速度

C．地球表面各处具有相同大小的向心加速度

D．地球表面各处的向心加速度方向都指向地球球心

4．匀速圆周运动的向心加速度的大小与线速度、角速度、圆周半径的关系。

(1) 由a_n=知：r一定时，a_n∝v²；v一定时，a_n∝；a_n一定时，v²∝r；

(2) 由a_n=rω²知：r一定时，a_n∝ω²；ω一定时，a_n∝r，a_n一定时，。

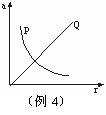例4　 如图所示为质点P、Q做匀速圆周运动时向心加速度随半径变化的图线，表示质点P的图线是双曲线，表示质点Q的图线是过原点的一条直线。由图线可知(　　 )

A．质点P线速度大小不变

B．质点P的角速度大小不变

C．质点Q的角速度随半径变化

D．质点Q的线速度大小不变

解析　 根据图象提供的曲线的性质建立起质点做匀速圆周运动的向心加速度a随半径r变化的函数关系，再根据这个函数关系，结合向心加速度的计算公式作出判断。答案：A

点评 在利用图象解决物理问题时，要注意充分挖掘图象中所携带的信息，如：一个量随另一个量如何变化；变化的确切数量关系；斜率多大，其物理意义是什么?截距、面积各有什么意义等。同时还要注意把物理图象和具体的物理情景结合起来，考虑应该选取哪一个规律或公式解决问题。

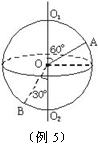
例5　 如图所示，一球体绕轴O₁O₂以角速度ω旋转，A、B为球体上两点。下列说法中正确的是(　　 )

A．A、B两点具有相同的角速度

B．A、B两点具有相同的线速度

C．A、B两点具有相同的向心加速度

D．A、B两点的向心加速度方向都指向球心

解析　 A、B都随球体一起绕轴O₁O₂旋转，转一周所用时间相等，故角速度相等，有ω_A=ω_B=ω，A做圆周运动的轨道平面与轴垂直，交点为圆心，故A的轨道半径r_A=sin60°，同理，B的轨道半径r_B=sin30°，所以两者的线速度　 v_A=r_Aω=ω ，v_B=r_Bω=ω ，显然，v_A>v_B 。

两者的向心加速度 a_A=r_Aω²=ω² ， a_B=r_Bω²=ω²　 ，显然，两者的向心加速度也不相等，又两者的向心加速度指向各自的圆心，所以并不指向球心。答案：A

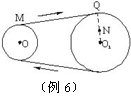
例6　 如图所示，O、O₁为两个皮带轮，O轮的半径为r，O₁轮的半径为R，且R>r，M点为O轮边缘上的一点，N点为O₁轮上的任意一点，当皮带轮转动时(设转动过程中不打滑)，则(　　 )

A．M点的向心加速度一定大于N点的向心加速度

B．M点的向心加速度一定等于N点的向心加速度

C．M点的向心加速度可能小于N点的向心加速度

D．M点的向心加速度可能等于N点的向心加速度

解析 　因为两轮的转动是通过皮带传动的，而且皮带在传动过程中不打滑，故两轮边缘各点的线速度大小一定相等。在大轮边缘上任取一点Q，因为R>r，所以由a=可知，a_Q<a_M ，再比较Q、N两点的向心加速度的大小，因为Q、N是在同一轮上的两点，所以角速度ω相等。又因为R_Q>R_N，则由a=ω²r可知，a_Q>a_N ，综上可见，a_M>a_N ，因此A选项正确。

[同步检测]

3．向心加速度

⑴ 定义：做匀速圆周运动的物体，加速度指向圆心，这个加速度称为向心加速度。

⑵ 方向：总是沿着圆周运动的半径指向圆心，即方向始终与运动方向垂直，方向时刻在改变，不论加速度a_n的大小是否变化，a_n的方向是时刻改变的，所以圆周运动一定是变加速度的运动。

⑶ 几种表达式：

除了教材P51介绍的a_n=、a_n=rω²外，向心加速度还有另外几种形式：

联系ω==2πf，代入a_n=rω²可得：a_n=r和a_n=4π²f²r，再根据v=ωr可得：a_n=vω

至此，我们常遇到的向心加速度表达式有以上五种。

由向心加速度的表达式和匀速圆周运动的特点可知：匀速圆周运动是一个加速度大小不变、方向时刻变化的变加速曲线运动。

例1　 一质点沿着半径r = 1 m的圆周以n = 1 r/s的转速匀速转动，如图，试求：

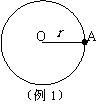(1) 从A点开始计时，经过s的时间质点速度的变化；

(2) 质点的向心加速度的大小。

解析　 (1) 求出s的时间连接质点的半径转过的角度是多少；

(2) 求出质点在A点和s末线速度的大小和方向。

(3) 由矢量减法作出矢量三角形。

(4) 明确边角关系，解三角形求得Δv的大小和方向。

(5) 根据a_n=或a_n=ω²r求出向心加速度的大小。

答案 (1)Δv=2π m/s　 方向与OA连线成45°角指向圆心O　 (2)a=4π²m/s²

例2　 一小球被细线拴着做匀速圆周运动，其半径为R，向心加速度为a，则(　　 )

A．小球相对于圆心的位移不变

B．小球的线速度为

C．小球在时间t内通过的路程s=

D．小球做圆周运动的周期T=2π

解析　 小球做匀速圆周运动，各时刻相对圆心的位移大小不变，但方向时刻在变

由a=得v²=Ra，所以v= ， 在时间t内通过的路程s=vt=t　

做圆周运动的周期T====2π

答案：BD

⑷ 物理意义：

因为向心加速度方向始终指向圆心，与线速度方向垂直，只改变线速度的方向，不改变其大小，所以向心加速度是描述线速度方向变化快慢的物理量。

例3　 关于向心加速度，下列说法正确的是(　　 )

A．它是描述角速度变化快慢的物理量

B．它是描述线速度大小变化快慢的物理量

C．它是描述线速度方向变化快慢的物理量

D．它是描述角速度方向变化快慢的物理量

解析　 (1) 从匀速圆周运动的特点入手思考，匀速圆周运动其角速度不变，线速度的大小不变，线速度方向总是与半径垂直在不断变化，半径转过多少度，线速度的方向就改变多少度。故答案为C

思考　 从公式a_n=看，向心加速度与圆周运动的半径成反比；从公式a_n=rω²看，向心加速度与半径成正比，这两个结论是否矛盾？

分析　 我们注意到，在公式y=kx中，说y与x成正比的前提条件是k为定值。同理，在公式a_n=中，当v为定值时，a_n与r成反比；在公式a_n=rω²中，当ω为定值时，a_n与r成正比。因此，这两个结论是在不同的前提下成立的，并不矛盾。

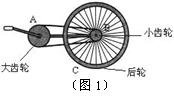
思考　 如图1所示，自行车的大齿轮、小齿轮、后轮三个轮子的半径不一样，它们的边缘上有三个点A、B、C。其中哪两点向心加速度的关系适用于“向心加速度与半径成正比”，哪两点适用于“向心加速度与半径成反比”？作出解释。

分析　 大、小齿轮用链条相连，因此两轮边缘上的点线速度必相等，即有v_A=v_B=v。又a_A=，a_B=，所以A、B两点的向心加速度与半径成反比。

小齿轮与后轮共轴，因此两者有共同的角速度，即有ω_B=ω_C=ω，又a_B=r_Bω²，a_C=r_Cω²，所以B、C两点的向心加速度与半径成正比。

2．曲线运动速度增量Δv=v₂-v₁的求法

(1) 将矢量减法转化为矢量加法计算：如Δv₂=v₂-v₁=v₂+(-v₁)(-v₁就是与矢量v₁大小相等方向相反的量)，运用平行四边形法则可以求得。

(2) 矢量三角形法：将表示v₁、v₂的两个矢量，保持原来的大小和方向，使它们的始端重合，然后从初态矢量v₁的箭头端向末态矢量v₂的箭头端做一有向线段，此有向线段就是所要求的矢量Δv=v₂-v₁。

1．研究匀速圆周运动向心加速度的方法

(1) 观察分析自然现象以及日常生活中的匀速圆周运动实例，研究做匀速圆周运动的物体的受力情况，将牛顿第二定律迁移到匀速圆周运动这一曲线运动中来，获得向心加速度的大小和方向。

(2) 根据加速度的定义a=，求出匀速圆周运动中速度的增量Δv的大小和方向，运用微积分的思想，求出向心加速度的大小和方向。

4．在圆周运动中，线速度、角速度的关系是　　 　。

[同步导学]

3．在曲线运动中，速度变化量Δv与始末两个速度v₀、v的关系：_____________________________。

2．在直线运动中，取初速度v₀方向为正方向，如果速度增大，末速v大于初速度v₀，则Δv=v－v₀　　 0(填“>”或“<”)，其方向与初速度方向　　　 ；如果速度减小，Δv=v－v₀　　 0，其方向与初速度方向　　　 。

1．加速度是表示　　　　　 的物理量，它等于　　　　　　　　　 的比值。在直线运动中，v₀表示初速度，v表示末速度，则速度变化量Δv=　　　 。加速度公式a=　　　 ，其方向与速度变化量方向　　　 。

14．⑴　 ⑵　 　　15．轨迹为一半径的圆周