1、以保证这部分学生有一个平等的发展的机会，享受成功的喜悦。但不能影响考试的公平性。

2、(5)如图12，在△ABC中，∠A=70°，

∠B=50°，CD平分∠ACB。

求∠ACD的度数。　　　　　　　　　　　　　　　　　 图13

[得失谈]　 《数学课程标准》提出的“尊重学生的个体差异，满足多样化的学习需要”、“不同的人在数学上得到不同的发展”。这道附加题就是为学习有困难的学生设计的一道人文关怀题，是一道“扶贫题”，为学习困难学生创设更多获得成功的机会，达到“脱贫”的目的，同时“全卷总分不超过90分”，保证这种“脱贫”不会“致富”，不会产生新的不公平。

中考自选题的增设，关注了学生的个性差异，使每个学生都能得到充分的发展。使“不同的人在数学上得到不同的发展”这一新理念在中考评价中得到较好的体现，但由于自选题的形式和目的不同，针对的是一部分学生的实际而增设，因此在命制自选题中应注意：

例10、(2005年泉州市中考试题)

友情提示：请同学们做完上面考题后，再认真检查一遍，估计一下你的得分情况，如果你全卷得分低于90分(及格线)，则本题的得分将计入全卷部分，但计入后全卷总分最多不超过90分；如果你全卷得分已经达到或超过90分，则本题的得分不计入全卷总分。

1、(5分)解方程：2x+1=7

例9、(2002年杭州市中考试题)如图11，

⊙O与⊙O₁外切于点T，PT为其内公切线，

AB为其外公切线，且A、B为切点，AB与PT　　　　　　 　　　　　图12

相交于点P，根据图中给出的已知条件及线段，请写出一个正确结论，并加以证明。

(本题将按正确结论的难易度评分)(本题12分)

[得失谈]　 探索性自选题能给学生留有充分的探索和发现的空间，能使不同水平的学生都能在不同层次的发现，较好地体现了“让不同的人在数学中得到不同的发展”这一基本理念。同时也加强了对学生数学学习能力的评价力度，这种评价方式充分体现了素质教育的要求。但这类试题对学生的心理素质也提出了新的要求，学生要在短时间内作出决策，并且试题结论的难易程度学生也难以把握，心中无底。再加上学生结论的发现又是开放性的，结论不一定在试卷评分标准的范围之内，教师阅卷时,评分标准不易掌握，难度也较大。

例8、(2005年浙江省湖州市中考试题)自选题(本题有2个小题，共10分)

注意：本题为自选题，供考生选做。自选题得分将

计入本学科的总分，但考生所得总分最多为120分。

(本小题4分)如图10，四边形ABCD和BEFG

均为正方形，则=　　　　 。(结果不取近似值)　

图11

(本小题6分)某高速公路收费站，有m(m>0)辆汽车排队等候收费通过。假设通过收费站的车流量(每分钟通过的汽车数量)保持不变，每个收费窗口的收费检票的速度也是不变的。若开放一个收费窗口，则需20分钟才可能将原来排队等候的汽车以及后来接上来的汽车全部收费通过；若同时开放两个收费窗口，则只需8分钟也可将原来排队等候的汽车以及后来接上来的汽车全部收费通过。若要求在3分钟内将排队等候收费的汽车全部通过，并使后来到站的汽车也随到随时收费通过，请问至少要同时开放几个收费窗口？

[得失谈] 　附加题的设置，从分值上看已超出了满分的值，有利方面是对部分学生创新意识和创新能力的肯定和鼓励，但也有一些影响考试的公平性。例如A、B两考生，A同学正题得116分，附加分得4分，则总分为满分120分，B同学正题得120分，附加分题也得4分，但总分也是120分，实际水平B同学优于A同学，但从结果上看两个同学的实际水平就一样了。

例4、(2005年大连市课改实验区试题)

如图2，操作：把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上(CG>BC)，取线段AE的中点M，探究：线段MD，MF的关系，并加以证明。

说明：(1)如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路写出来(要求至少写3步)；(2)在你经历说明(1)的过程后，可以从下列①，②，③中选取一个补充或更换已知条件，完成你的证明。

注意：选取①完成证明得10分；选取②完成证明得7分；选取③完成证明得5分。

①DM的延长线交CE于点N，且AD=NE；②将正方形CGEF绕点C逆时针旋转45°(如图3)，其他条件不变；③在②的条件下，且CF=2AD。

图2　　　　　　　　　　　　　　 图3

例5、(2005年广西南宁实验区试题)

(本题有A、B两类题，A类题满分7分，B类题满分10分，请你选择其中一类证明。)

(A类)如图4，DE⊥AB，DF⊥AC，垂足分别为E、F，请你从下面三个条件中，再选出两个作为已知条件，另一个为结论，推出一个正确的命题(只需写出一种情况)。

①AB=AC　 ②BD=CD　 ③BE=CF

已知DE⊥AB，DF⊥AC，垂足分别为

E、F，　　　 =　　　 ，　　　 =　　　 。

求证：

证明：　　　　　　　　　　　　　　　　　　　　　　　　 图4

(B类)如图5，EG∥AF，请你从下面三个条件中，再选两个作为已知条件，另一个为结论，推出一个正确的命题(只需写出一种情况)。

①AB=AC　 ②GD=CD　 ③BE=CF

已知：EG∥AF，　　　 =　　　 ，　　　 =　　　 。

求证：

证明：　　　　　　　　　　　　　　　　　　　　　　　

例6、(2005年浙江绍兴市中考试题)　　　　　　　　　　　 图5

(以下两小题选做一题，第(1)小题满分5分，第(2)小题满分3分，若两小题都做，以第(1)小题计分

(1)将一副三角板如图6叠放，

则左右阴影部分面积之比S₁:S₂等于

　　　 　。

(2)将一副三角板如图7放置，

则上下两块三角板面积之比A₁:A₂

等于　　　 　　。　　　　　　　　　　　　　 图6　　　　　　　 图7

例7、(2005年绍兴市中考压轴题)(本题满分14分)

(以下两小题选做一题，第(1)小题满分14分，第(2)小题满分10分，若两小题都做，以第(1)小题计分)

选做第　　　　　 　小题。

(1)一张矩形纸片OABC平放在平面直角

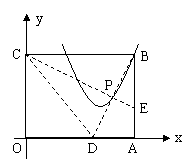坐标系内，O为原点，点A在x轴的正半轴上，

点C在y轴的正半轴上，OA=5，OC=4。

①如图8，将纸片沿CE对折，点B落在x轴上的点D处，求点D的坐标；

②如图8，在①中，设BD与CE的交点为P，若点P，B在抛物线y=x²+bx+c上，求b,c值；　　　　　　　

图8

③若将纸片沿直线对折，点B落在坐标轴上的

点F处，与BF的交点为Q。若点Q在②的抛物线上，

求的解析式。

(2)一张矩形纸片OABC平放在平面直

角坐标系内，O为原点，点A在x轴的正半轴　　　　　　　　　　

上，点C在y轴的正半轴上，OA=5，OC=4。

①如图9，求直线AC的解析式；

②如图9，若M为AC与BO的交点，点M在抛物线　　　　　　　　　　

y=-x²+kx上，求k的值；

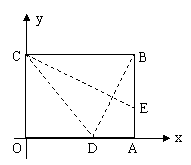
③如图10，将纸片沿CE对折，点B落在x轴上

的点D处，试判断点D是否在②的抛物线　　

上，并说明理由。　　　　　　　　　　　　　　　

图10　　　　　　 　　　　　　　　　　　　　　　　　

[得失谈]　 新课程倡导“不同的人在数学上得到不同的发展”，注重人文关怀，尊重各类学生在数学学习中的发展权利，使不同层次的学生根据自身的实际情况选取不同起点的问题，获得成功，享受成功的喜悦。但这类题，由于不同的起点，对应着不同的分值，这也对考生来讲是一次心理素质方面的考验，学生虽然有选择的权利，但更要有自己在短时间内作出决策的气质， 在实际考试中有部分优等生当初选择了(1)后，做题遇到困难时，且失去了勇气和信心，没有迎着困难上，而是退下来去选择(2)，不但失去了得分，更失去了应有的一种精神。

例1、(2005年山东省潍坊市学业考试试题)(第14、15两题为选做题，只须做(A)、(B)题中的一个即可，若两题都做，只以(A)题计分)

(A题)盒子里装有大小形状相同、质地均匀的3个白球和2个红球，搅匀后从中摸出一个球，放回搅匀后，再摸出第二个球，则取出的恰是两个红球的概率是　　　　　　　 。

(B题)已知一次函数y=2x-5的图像与反比例函数y=的图像交于第四象限的一点P(a,-3a)，则这个反比例函数的解析式是　　　　　　 。

(A题)一次数学测验以后，张老师根据某班成绩绘制了如图1所示的扇形统计图(80-89分的百分比因故模糊不清)，若80分以上(含80分)为优秀等级，则本次测验这个班的优秀率为　　　　　　 。

(B题)某电视台在某一晚上黄金时段的3min

内插播长度为20s和40s的两种广告，20s广告每次

收费6000元，40s广告每次收费10000元，若要求

每种广告播放不少于2次，且电视台选择收益最大

的播放方式，则在这一天黄金时段3min内插播广告

的最大收益是　　　　　 元。　　　　　　　　　　　　　　　　　 图1

例2、(2005年武汉市中考试题)(本题共有A、B两小题，请你只选择一题作答)

A、请你写出一个能分解的二次四项式并把它分解　　　　　　　　

B、用计算器计算：sina40º=　　　　　 (精确到0.01)

[得失谈]　 A题与B题虽然考查的难度相当，但由于考查的知识点不同和能力要求不一样，学生在数学学习中所掌握的知识水平和能力水平的角度不一致，这样有利于学生可以根据自己的喜好和个性特点，选择适合自己实际的一题，提高自己的成功率。这样的试题为学生提供了更能展示自我的平台，使学生的个性得到了有效地展示。例2中的提示欠明确，若学生两题都做，阅卷时怎样给分，应有客观的规定。

例3、(2005年浙江省丽水市中考题)(请在下面给出的二个小题中选做一小题，每小题都答，按得分高的给分)

(1)计算：(-2)°+4×(-)

(2)计算：2(x+1)-x

[得失谈]　 本题中的提示“若每小题都答，按得分高的给分”，实际上给学生起了一个导向作用，相仿于要求学生两题都做，增加了相应的题量。但从另一方面看也体现了人文关怀，尽可能地给学生的得分，增加了学生成功的机会。

35．英国和美国的代议制是资本主义世界最具代表性的政治制度，下列对其表述和评价正确的是：

A．它们都是资产阶级民主政治　　　B．美国的代议制优于英国代议制

C．美国的政府首脑是民选的，而英国的政府首脑是世袭的

D．美国贯彻“分权制衡”原则，而英国不是