
2.类比推理:通过两类事物的相似性或一致性,用一类事物的性质去推测另一类事物的性质,得出一个明确的结论.常见的有结论类比和方法类比.
1.归纳推理:主要应用于先由已知条件归纳出一个结论,并加以证明或以推理作为题目的已知条件给出猜测的结论,并要求考生会应用或加以证明.
7.已知: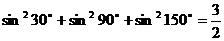

通过观察上述两等式的规律,请你写出一般性的命题:
__________________________________________= 并给出( * )式的证明。
并给出( * )式的证明。
一般形式: 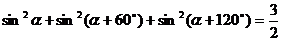
证明 左边 = 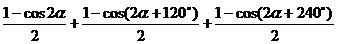
= 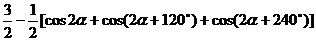
= 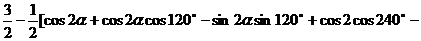

=  =
= 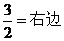
∴原式得证
(将一般形式写成
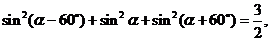
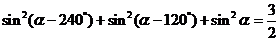 等均正确。)
等均正确。)
例1.通过计算可得下列等式:
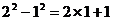

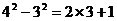
┅┅
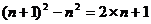
将以上各式分别相加得:
即:
类比上述求法:请你求出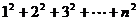 的值..
的值..
[解] 

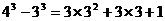 ┅┅
┅┅
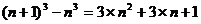
将以上各式分别相加得:
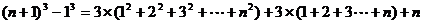
所以: 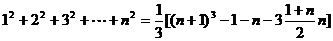
6.在等差数列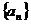 中,若
中,若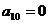 ,则有等式
,则有等式
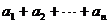
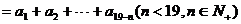 成立,类比上述性质,相应地:在等比数列
成立,类比上述性质,相应地:在等比数列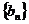 中,若
中,若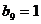 ,
,
则有等式
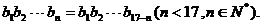 成立.
成立.
5.依次有下列等式: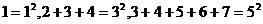 ,按此规律下去,第8个等式为 8+9+10+11+12+13+14+15+16+17+18+19+20+21+22=
,按此规律下去,第8个等式为 8+9+10+11+12+13+14+15+16+17+18+19+20+21+22=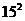 。
。
4.若数列{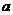
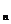 },(n∈N
},(n∈N )是等差数列,则有数列b
)是等差数列,则有数列b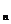 =
=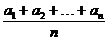 (n∈N
(n∈N )也是等差数列,类比上述性质,相应地:若数列{c
)也是等差数列,类比上述性质,相应地:若数列{c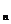 }是等比数列,且c
}是等比数列,且c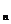 >0(n∈N
>0(n∈N ),则有d
),则有d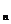 =______
=______  ______ (n∈N
______ (n∈N )也是等比数列。
)也是等比数列。
3. 由①正方形的对角线相等;②平行四边形的对角线相等;③正方形是平行四边形,根据“三段论”推理出一个结论,则这个结论是 ( A )
(A) 正方形的对角线相等 (B) 平行四边形的对角线相等
(C) 正方形是平行四边形 (D)其它
2.在平面几何里,有勾股定理:“设△ABC的两边AB,AC互相垂直,则AB2+AC2=BC2”拓展到空间,类比平面几何的勾股定理,“设三棱锥A-BCD的三个侧面ABC、ACD、ADB 两两相互垂直,则可得” ( C )
(A)AB2+AC2+ AD2=BC2+
CD2 + BD2 (B)
(C)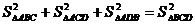 (D)AB2×AC2×AD2=BC2 ×CD2 ×BD2
(D)AB2×AC2×AD2=BC2 ×CD2 ×BD2
1. 观察下列数的特点
1,2,2,3,3,3,4,4,4,4,… 中,第100项是( C )
(A) 10 (B) 13 (C) 14 (D) 100
解析 . 由规律可得:数字相同的数依次个数为
1,2,3,4,… n 由 ≤100 n ∈
≤100 n ∈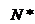 得,n=14,所以应选(C)
得,n=14,所以应选(C)
7.创新性问题
例9(2007北京理)(本小题共13分)已知集合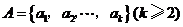 ,其中
,其中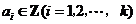 ,由
,由 中的元素构成两个相应的集合:
中的元素构成两个相应的集合: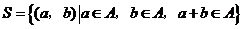 ,
,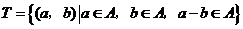 .
.
其中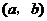 是有序数对,集合
是有序数对,集合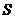 和
和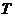 中的元素个数分别为
中的元素个数分别为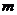 和
和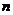 .
.
若对于任意的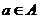 ,总有
,总有 ,则称集合
,则称集合 具有性质
具有性质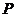 .
.
(I)检验集合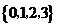 与
与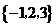 是否具有性质
是否具有性质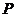 并对其中具有性质
并对其中具有性质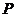 的集合,写出相应的集合
的集合,写出相应的集合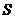 和
和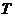 ;
;
(II)对任何具有性质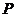 的集合
的集合 ,证明:
,证明: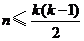 ;
;
(III)判断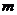 和
和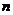 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
(I)解:集合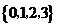 不具有性质
不具有性质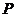 .
.
集合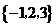 具有性质
具有性质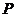 ,其相应的集合
,其相应的集合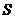 和
和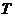 是
是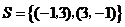 ,
,
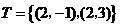 .
.
(II)证明:首先,由 中元素构成的有序数对
中元素构成的有序数对 共有
共有 个.
个.
因为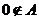 ,所以
,所以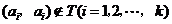 ;
;
又因为当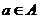 时,
时, 时,
时, ,所以当
,所以当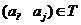 时,
时, .
.
从而,集合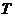 中元素的个数最多为
中元素的个数最多为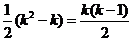 ,
,
即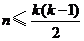 .
.
(III)解: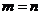 ,证明如下:
,证明如下:
(1)对于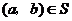 ,根据定义,
,根据定义,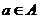 ,
,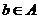 ,且
,且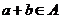 ,从而
,从而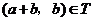 .
.
如果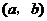 与
与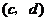 是
是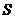 的不同元素,那么
的不同元素,那么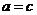 与
与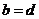 中至少有一个不成立,从而
中至少有一个不成立,从而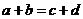 与
与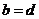 中也至少有一个不成立.
中也至少有一个不成立.
故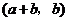 与
与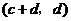 也是
也是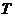 的不同元素.
的不同元素.
可见,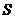 中元素的个数不多于
中元素的个数不多于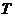 中元素的个数,即
中元素的个数,即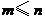 ,
,
(2)对于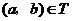 ,根据定义,
,根据定义,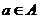 ,
,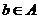 ,且
,且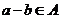 ,从而
,从而 .如果
.如果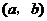 与
与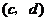 是
是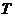 的不同元素,那么
的不同元素,那么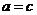 与
与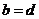 中至少有一个不成立,从而
中至少有一个不成立,从而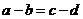 与
与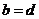 中也不至少有一个不成立,
中也不至少有一个不成立,
故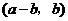 与
与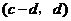 也是
也是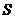 的不同元素.
的不同元素.
可见,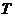 中元素的个数不多于
中元素的个数不多于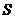 中元素的个数,即
中元素的个数,即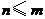 ,
,
由(1)(2)可知,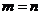 .
.
[专题突破]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com