17.(10分)

16.(10分)

15.(8分) 一路桥工人在长300米的隧道中，突然发现一汽车在离右隧道口150米处以速度v_o=54千米/小时向隧道驶来，由于隧道内较暗，司机没有发现这名工人。此时路桥工人正好处在向左、向右以某一速度匀速跑动都恰能跑出隧道而脱险的位置。问此位置距右出口距离是多少?他奔跑的最小速度是多大?

14.　 (6分)　 　　　　　　　　　　　　　　；　　　　　　　　　　　　　　　　　　　　　　　

13. (8分)(1)　　　　　　　　　　　　 ；

(2)　　　　　　　　　　　　　　　 ；

(3)　　　　　　　　　　　　　　　

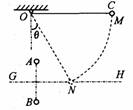
18.(10分)如图所示，在同一条竖直线上，有电荷量均为Q的A、B两个正点电荷，； GH是它们连线的垂直平分线．另有一个带电小球C，质量为m、电荷量为+q(可视为点电荷)，被长为l的绝缘轻细线悬挂于O点，现在把小球C拉起到M点，使细线水平且与 A、B处于同一竖直面内，由静止开始释放，小球C向下运动到GH线上的N点时刚好速度为零，此时细线与竖直方向的夹角= 30⁰．试求：

(1)在A、B所形成的电场中，M、N两点间的电势差，并指出M、N哪一点的电势高．

(2)若N点与A、B两个点电荷所在位置正好形成一个边长为a的正三角形，则小球运动到N

点瞬间，轻细线对小球的拉力F_T(静电力常量为k).

解析：(1)带电小球C在A、B形成的电场中从M点运动到N点的过程中，重力和电场力做功，但合力功为零，则　　 (3分)

所以　　 　　　　　　　　

即M、N两点间的电势差大小，且N点的电势高于M点的电势．(1分)

(2)在N点，小球C受到重力mg、细线的拉力F_T以及A和B分别对它的斥力F_A和F_B四个力的作用如图所示，且沿细线方向的合力为零．则(3分)

又　 (2分)

得　 (1分)

2010届高三月考答卷(三)

物 理

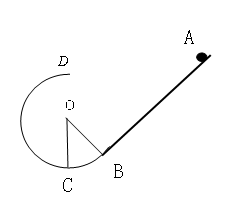
17.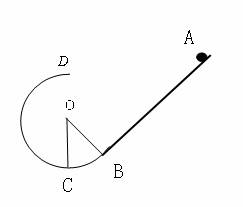(10分)如图，竖直放置的斜面下端与光滑的圆弧轨道BCD的B端相切，圆弧半径为R，∠COB=q ，斜面倾角也为q ，现有一质量为m的小物体从斜面上的A点无初速滑下，且恰能通过光滑圆形轨道的最高点D.已知小物体与斜面间的动摩擦因数为m，求：(1)AB长度l应该多大。(2)小物体第一次通过C点时对轨道的压力多大。

［解析］(1)因恰能过最高点C：

　　　　　 　　　( 1)　　　　 2分

　 (2)　 1分

　　　 物体从A运动到C全程，由动能定理：

(3) 2分　

联立求得：　　　 1分

(2)物体从C运动到D的过程，设C点速度为，由机械能守恒定律：

　　 (4 )　　 2分

物体在C点时：　　 　(5)　 1分

联立求得： 由牛顿第三定律可知，物体对轨道的压力是.　　 1分

16．(10分)地球以角速度绕地轴自转，一只热气球相对地面静止在赤道上空(不计气球离地高度)，已知地球半径为R，在距地面h高处的圆形轨道上有一颗人造地球卫星，设地球质量为M，热气球的质量为m，人造地球卫星的质量为m₁，根据上述条件，有一位同学列出了以下两个式子：

对热气球有：　　　　　　　　　　　　　　 (1)

对人造地球卫星有：　　 (2)

进而求出了人造地球卫星绕地球运行的角速度

这两个式子中有一个是错误的，找出来，并说明理由。现补充一个条件：已知第一宇宙速度为v₁,求距地h处的人造地球卫星绕地球运行的角速度

［解析］第一个等式(对热气球)不正确，因为热气球不同于人造卫星，热气球静止在空中是因为浮力与重力平衡，(4分)

(2))若利用第一宇宙速度v₁，有　 (4分)

与第二个等式联立可得　　 (2分)

15．(8分)一路桥工人在长l=300米的隧道中，突然发现一汽车在离右隧道口s=150米处以速度v_o=54千米/小时向隧道驶来，由于隧道内较暗，司机没有发现这名工人。此时路桥工人正好处在向左、向右以某一速度匀速跑动都恰能跑出隧道而脱险的位置。问此位置距右出口距离x是多少?他奔跑的最小速度是多大?

［解析］

工人朝右隧道口奔跑，恰能脱险：　　　　 (1)　　　　　 3分

　　　　 工人朝左隧道口奔跑，恰能脱险：(2)　　　 3分

联立可得；　 　　　　　　　2分

14.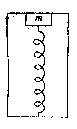(6分)如图，在一箱中，用压缩的轻弹簧将金属块卡住，在箱的上顶板和下底板装有压力传感器(顶面和底面均水平)，箱可以沿竖直轨道运动，当箱以a=2.0m/s²的加速度竖直向上做匀减速运动时，上顶板的压力传感器显示的压力为6.0N，下底板的压力传感器显示的压力为10.0N.(取g=10m/s²)若上顶板压力传感器的示数是下底板压力传感器的示数的一半，则箱做　　　　 运动。若上顶板压力传感器的示数为零，下底板示数恒定，则箱沿竖直方向运动的可能情况为　　　　　　　　　　　　　　　　　 　　(写出运动特征及加速度的范围)

［解析］　(　弹簧形变不变，下底板传感器示数不变)匀速直线运动 ；(3分)

(恰与上顶面脱离或已脱离)向上匀加速或向下匀减速直线运动，a≥10m／s² (3分)