
17.解:(Ⅰ)∵ ·
· =
= ·
· .
.
∴bccosA=accosB,即bcosA=acosB …………………………………………1分
由正弦定理得 sinBcosA=sinAcosB
∴sin(A-B)=0 ………………………………………………………………… 2分
∵-π<A-B<π ………………………………………………………………3分
∴A-B=0,∴A=B …………………………………………………………4分
(Ⅱ)∵ ·
· =1,∴bccosA=1…………………………………………… 5分
=1,∴bccosA=1…………………………………………… 5分
由余弦定理得 bc· =1,即b2+c2-a2=2 …………………6分
=1,即b2+c2-a2=2 …………………6分
∵由(Ⅰ)得a=b,∴c2=2,∴c= ……………………………………8分
……………………………………8分
(Ⅲ)∵| +
+ |=,∴|
|=,∴| |2+|
|2+| |2+2
|2+2 ·
· =6 ………9分
=6 ………9分
即c2+b2+2=6
∴c2+b2=4 ……………………………………………………………………… 10分
∵c2=2∴b2=2,b= ∴△ABC为正三角形 …………………………………11分
∴△ABC为正三角形 …………………………………11分
∴S△ABC=×( )2= ………………………………………………… 12分
)2= ………………………………………………… 12分
已知向量

(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)若 的取值范围.
的取值范围.
16.(1)若原函数有意义,则
故
(2)因为
故函数f(x)的最大值为 恒成立,只需
恒成立,只需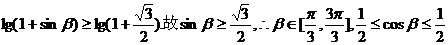
故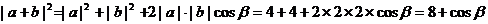
故
要得到函数 +1的图象,只需将函数
+1的图象,只需将函数 的图象作下列平移,其
的图象作下列平移,其
中正确的平移是 (6.A )
A.按 平移 B.按
平移 B.按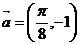 平移
平移
C.按 平移 D.按
平移 D.按 平移
平移
已知锐角△ABC中,内角A、B、C的对边分别为a、b、c,向量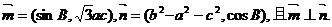
(1)求角B的大小;
(2)若 边上的高的最大值.
边上的高的最大值.
解:(I)
 …………2分
…………2分

 …………6分
…………6分
(II) ,
,
由余弦定理得:
 时取等号 …………8分
时取等号 …………8分
于是 …………10分
…………10分

∴AC边上的高的最大值为 …………12分
…………12分
设i,j是平面直角坐标系分别与x轴、y轴正方向相同的两个单位向量,已知a=3i-j,
b=mi+2j(m为实数),且a⊥b,则|b|= 
已知△ABC的面积为
(1)求 的值;
的值;
(2)求 的值.
的值.
解:(1) , ①…………………2分
, ①…………………2分
又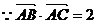 ,
,
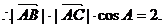 ②……………… 4分
②……………… 4分
由①、②得 ……………………………………………………… 6分
……………………………………………………… 6分
(2)
 ……………………………………………………………… 8分
……………………………………………………………… 8分
 …………………………………………………………………… 10分
…………………………………………………………………… 10分

 …………………………………
…………………………………
已知向量 ,向量
,向量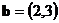 ,且a与b的夹角为锐角,则实数m的取值范围为
,且a与b的夹角为锐角,则实数m的取值范围为  。
。
在△ABC中,a、b、c分别是角A、B、C的对边,C=2A,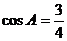 .
.
(1)求 的值;
的值;
(2)若 ,求边AC的长.
,求边AC的长.
解:(1) , (2分)
, (2分)
 (4分)
(4分)

 (6分)
(6分)
(2)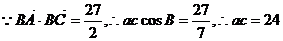 ①
①
又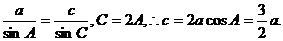 ②
②
由①②解得a=4,c=6 (10分)
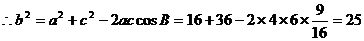 ,
,
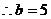 ,即边AC的长为5. (12分)
,即边AC的长为5. (12分)
已知两个非零向量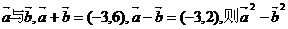 = (C )
= (C )
A.-3 B.-24 C.21 D.12
已知A、B两点的坐标分别为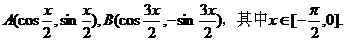
(Ⅰ)求| |的表达式;
|的表达式;
|
 (O为坐标原点),求
(O为坐标原点),求 的值;
的值;
(Ⅲ)若 ,求函数
,求函数 的最大值和最小值。
的最大值和最小值。
解:(I) ……………………1分
……………………1分
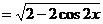 ……………………………………………………2分
……………………………………………………2分
=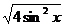 …………………………………………………………3分
…………………………………………………………3分
= …………………………………………4分
…………………………………………4分
(Ⅱ) ………………………………………………5分
………………………………………………5分

又 ………………………………7分
………………………………7分
 ………………………………………………………………8分
………………………………………………………………8分
(Ⅲ)
=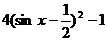 …………………………………………9分
…………………………………………9分
 ……………………………………………10分
……………………………………………10分
当sinx=0时, ………………………………………………11分
………………………………………………11分
当sinx=-1时, ……………
……………
已知A、B两点的坐标分别为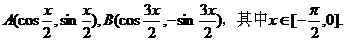
(Ⅰ)求| |的表达式;
|的表达式;
|
 (O为坐标原点),求
(O为坐标原点),求 的值;
的值;
(Ⅲ)若 ,求函数
,求函数 的最小值。
的最小值。
解:(I) ……………………1分
……………………1分
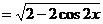 ……………………………………………………2分
……………………………………………………2分
=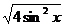
= …………………………………………3分
…………………………………………3分
(Ⅱ) ………………………………………………4分
………………………………………………4分

又 ………………………………6分
………………………………6分
 ………………………………………………………………7分
………………………………………………………………7分
(Ⅲ)
= …………………………………………8分
…………………………………………8分
 ……………………………………………9分
……………………………………………9分
当 时,
时, 的最小值为-4
的最小值为-4 2,此时
2,此时 ………………10分
………………10分
当 时,
时, 的最小值为4+8
的最小值为4+8 ,此时
,此时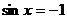 …………………11分
…………………11分
当 时,
时, 的最小值为0,此时
的最小值为0,此时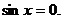 ……………………12分
……………………12分
已知△ABC中, =1,若△ABC的面积为S,且
=1,若△ABC的面积为S,且
(I)求角B的取值范围;
(II) 的取值范围.
的取值范围.
解:(本小题满分12分)
(I)
 …………………………………………①
…………………………………………①
又 ……………………………………②
……………………………………②
∴由②①得tanB=2S
又

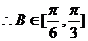 ……………………………………………………6分
……………………………………………………6分
(II)


若 ,则一定有B ( )
,则一定有B ( )
A.a与 b共线 B.a⊥b
C.a与 b的夹角为45° D.|a|=|b|
在△ABC中,角A、B、C的对边分别为a、b、c,若 ·
· =
= ·
· =1.
=1.
(Ⅰ)求证:A=B;
(Ⅱ)求边长c的值;
|
 +
+ |=,求△ABC的面积.
|=,求△ABC的面积.4.设AB垂直平分线交AB于M,


已知函数
(1)求函数 的定义域;
的定义域;
(2)若 是两个膜长为2的向量a,b的夹角,且不等式
是两个膜长为2的向量a,b的夹角,且不等式 对于定义域内的任意实数x恒成立,求|a+b|的取值范围.
对于定义域内的任意实数x恒成立,求|a+b|的取值范围.
19.(1)设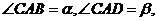
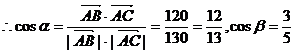 …………………………2分
…………………………2分

 ………………4分
………………4分
 …………………………………………………………6分
…………………………………………………………6分
(2)由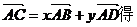
 ………………………………………………8分
………………………………………………8分
 ……………………………………………………10分
……………………………………………………10分
解得 ……………………………………………………12分
……………………………………………………12分
(由正弦定理求解,参照给分)
已知O是△ABC所在平面内的一定点,动点P满足 ,
, ,则动点P的轨迹一定通过△ABC的 ( .D
,则动点P的轨迹一定通过△ABC的 ( .D
)
A.内心 B.垂心 C.外心 D.重心
把函数 的图象按向量
的图象按向量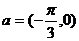 平移,所得曲线的一部分如图所示,则
平移,所得曲线的一部分如图所示,则 、
、 的值分别是 ( 8.D
)
的值分别是 ( 8.D
)
A.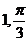 B.
B.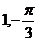
C. D.
D.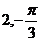
函数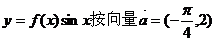 平移后,得到函数
平移后,得到函数 ,则
,则 是
是
(B )
A. B.2
B.2 C.
C.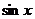 D.2
D.2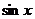
在△ABC中,∠B=45°,BC=3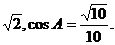
(Ⅰ)求△ABC的面积S;
(Ⅱ)求BC边上的中线长.
解(I) , …………2分
, …………2分

 …………4分
…………4分
 …………6分
…………6分
 …………8分
…………8分
(II)设BC边上的中线为AD,
则
 即中线的长为
即中线的长为
如图,P为△AOB所在平面上一点,向量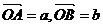 ,
, 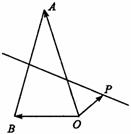
且P在线段AB的垂直平分线上,向量 。若|a|=3,
。若|a|=3,
|b|=2,则c·(a-b)的值为 ( )
A.5 B.3
C.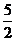 D.
D.
16、给出下列命题:
(1) ∥
∥ 的充要条件是存在唯一的实数
的充要条件是存在唯一的实数 使
使 =
=
 ;
;
(2)若α、β是第一象限角,且α>β,则cosα<cosβ;
(3)函数y=sin( x-
x-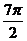 )是偶函数;
)是偶函数;
(4) 向量 与向量
与向量 的方向相反,是
的方向相反,是 与
与 是共线向量的充分不必要条件;
是共线向量的充分不必要条件;
(5)函数y=sin2x的图象向右平移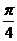 个单位,得到y=sin(2x-
个单位,得到y=sin(2x-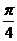 ))的图象.
))的图象.
其中正确的命题的序号是 . 34
如图,已知向量 ,
, ,
,
 ,且
,且 .(Ⅰ)试用
.(Ⅰ)试用 表示
表示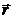 ;
;
(Ⅱ)若点
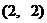 、
、
 ,O(0,0)求点
,O(0,0)求点 坐标.
坐标.
解:(Ⅰ)由题意得:  ,
, ,-------2分
,-------2分
又

∴
 -----------4分
-----------4分
解得:
 -----------6分
-----------6分
(Ⅱ) 由 可知:点
可知:点 分有向线段
分有向线段 所成的比为2,---8分
所成的比为2,---8分
设点
 ,则得:
,则得:
 ,
, ---------10分
---------10分
解得:
 ,
, ,
,
∴
点 坐标为
坐标为 .-----------12分
.-----------12分
命题p:向量 与向量
与向量 的夹角为钝角。命题q:
的夹角为钝角。命题q: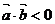 。则p是q的(B )
。则p是q的(B )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
已知 的面积
的面积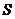 满足
满足 且
且 与
与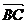 的夹角为
的夹角为 。
。
(1).求 的取值范围。
的取值范围。
(2).求函数 的值域。
的值域。
解:(1)因为
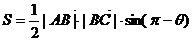 ---------------------------------3分
---------------------------------3分
所以3 ,由
,由 得
得 即
即 又
又 为
为 与
与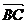 的夹角,所以
的夹角,所以 -----6分
-----6分
(2)
 ------------------9分
------------------9分
由 ,得
,得 ,---11分
,---11分
所以函数 的值域为
的值域为 。-----------------------------------12分
。-----------------------------------12分
已知向量m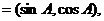 n
n , m
. n
, m
. n 分别为△ABC的三边a,b,c所对的角.
分别为△ABC的三边a,b,c所对的角.
(Ⅰ)求角C的大小;
(Ⅱ)若sinA, sinC, sinB成等比数列, 且 , 求c的值.
, 求c的值.
解:(Ⅰ) ∵ m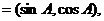 n
n , m
. n
, m
. n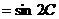 ,
,
∴sinAcosB+cosAsinB=sin2C 1分
即 sinC=sin2C 3分
∴ cosC=  4分
4分
又C为三角形的内角, ∴  6分
6分
(Ⅱ) ∵sinA,sinC,sinB成等比数列,
∴ sin2C=sinAsinB 7分
∴ c2=ab 8分
又 ,即
,即  9分
9分
∴ abcosC=18 10分
∴ ab=36 故 c2=36 ∴ c=6 12分
在△ABC中,角A、B、C所对应的边分别为a、b、c,锐角B满足
(I)求 的值;
的值;
(II)若a:b=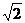 :1,求
:1,求 的值.
的值.
解:(I)∵锐角B满足 ,……………………(2分)
,……………………(2分)
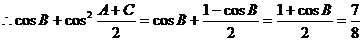 .……(7分)
.……(7分)
(II)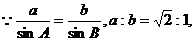

 如图,平面四边形ABCD中,AB=13,三角形ABC的面积为S△ABC=25,
如图,平面四边形ABCD中,AB=13,三角形ABC的面积为S△ABC=25,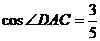 ,
, ,求
,求
(1)AC的长;
(2)cos∠BAD。
解:(1)
又S△ABC=25, 得
∴13x·cosα=120 ①
13x·sinα=50 ② …………………………4分
①2+②2 得:x=10 ……………………5分
AC=10 ………………………………6分
(2)设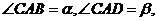
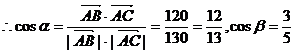 …………………………8分
…………………………8分

 ………………10分
………………10分
 ………………………………………………………
………………………………………………………
 如图,平面四边形ABCD中,AB=13,三角形ABC的面积为S△ABC=25,
如图,平面四边形ABCD中,AB=13,三角形ABC的面积为S△ABC=25,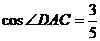 ,
, ,求
,求
(1)求cos∠BAD;
(2)设 的值.
的值.
7、已知点P分 所成的比是-3,则P1分
所成的比是-3,则P1分 所成的比是 ( C )
所成的比是 ( C )
(A) (B)
(B)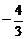 (C)
(C)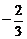 (D)
(D)
在 中,
中, ,若
,若 =5,则
=5,则 的面积等于(B )
的面积等于(B )
A B
B 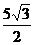 C
C
 D
D

13、△ABC中,已知b2-bc-2c2=0,a= ,cosA=
,cosA= ,则S△ABC =
,则S△ABC = 。
。
12、将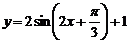 的图象按向量
的图象按向量 平移得到
平移得到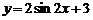 的图象,则
的图象,则 =(
=( ,2)。
,2)。
11、△ABC中,已知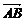 =(2,-1),
=(2,-1), =(3,1),则∠B=_135°__。
=(3,1),则∠B=_135°__。
22.解:(1)如图:由
得 ,
,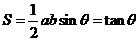
∵ ∴
∴ 而
而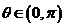
∴ ……………………………… 3分
……………………………… 3分
 ∴
∴ 


 ……………………… 5分
……………………… 5分
∵ ∴
∴
∴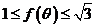
即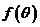 的值域为
的值域为 ……………………… 7分
……………………… 7分
(2)∵ ………… 9分
………… 9分
∴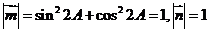


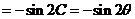 ……………………… 10分
……………………… 10分
∴
 ……………………… 11分
……………………… 11分
∵ ∴
∴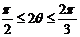
故当 时,
时, ,即
,即 的最大值为
的最大值为 。 …………
13分
。 …………
13分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com