14．若函数y = f ( x ) ( x∈R )满足f ( x + 2 ) = f ( x )，且x∈[– 1，1]时，f ( x ) = | x |，函数y =g ( x )是偶函数，且x∈( 0 , +∞)时，g ( x ) = | log3x |。则函数y = f ( x )图像与函数y = g ( x )图像的交点个数为_________________

3．已知甲盒内有大小相同的3个红球和4个黑球，乙盒内有大小相同的4个红球和4个黑

球，现从甲、乙两个盒内各任取2个球，则取出的4个球中恰有一个红球的概率是______

13．某中学在高一开设了数学史等4门不同的选项修课，每个学生必须选项修，且只从中选一门。该校高一的3名学生甲、乙、丙对这4门选课的兴趣相同，则3个学生选择了3

门不同的选修课的概率是__________________

12．如果有穷数列a1 , a2 , … , an (n为正整数)满足条件a1 = an , a2 = an–1…,an = a1,即ak = an–k+1 (k = 1 , 2 …, n )，我们称其为“对称数列”。设{bn}是项数为7的“对称数列”，其中b1 , b2 , b3 , b4成等差数列，且b1 = 2 , b2 + b4 = 16，依次写出{bn}的每一项____________

11．正方体ABCD-A1B1C1D1的各顶点均在半径为1的球面上，则四面体A1-ABC的体积

等于____________

10．函数y = cos x · sin的最小正周期是_______________________

9．函数f ( x ) = 2–x ( 0＜x≤3 )的反函数的定义域为____________________

8．编号为1，2，3，4，5的5人入座编号也为1，2，3，4，5的5个座位，至多有两人对

号入座的不同坐法有(　 )

　　　 A．109种　　　　　　　　　　 B．110种　　　　　　　　　　 C．108种　　　　　　　　　　 D．111种

第Ⅱ卷(非选择题　　　 共110分)

7．已知向量= ( 1 , 3 )，= ( 3 , n )若2–与共线，则实数n的值是(　 )

　　　 A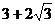．　　　　　　　 B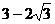．　　　　　　　　 C．6　　　　　　　　　　　　　　 D．9

6．若圆x2 + y2 – 2x + 4y = 0与直线x – 2y + a = 0相离，则实数a的取值范围是(　 )

　　　 A．– 2＜a＜8a＞8或a＜– 2　　　 　　　　　　　　　 B．a＞0或a＜– 10

C．– 10＜a＜0 　　　　　　　　　　　　　　　　　　　　　　　 D．a＞8或a＜– 2