
22、解:(I)在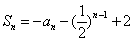 中,令n=1,可得
中,令n=1,可得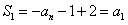 ,即
,即
当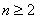 时,
时,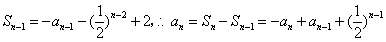 ,…… 2分
,…… 2分

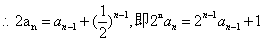 .
.
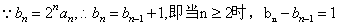 .
.
.
.
又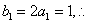 数列
数列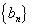 是首项和公差均为1的等差数列. ……………………4分
是首项和公差均为1的等差数列. ……………………4分
于是 .……………………5分
.……………………5分
(II)由(I)得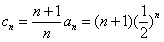 ,所以
,所以
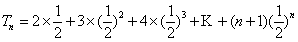
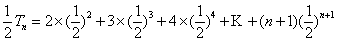
由①-②得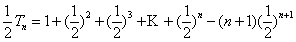
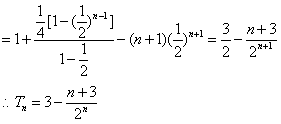
……………………8分
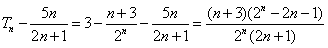
于是确定 的大小关系等价于比较
的大小关系等价于比较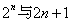 的大小
的大小
由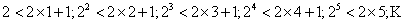
可猜想当 证明如下:……………………10分
证明如下:……………………10分
证法1:(1)当n=3时,由上验算显示成立。
(2)假设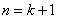 时
时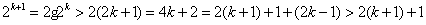
所以当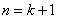 时猜想也成立
时猜想也成立
综合(1)(2)可知 ,对一切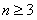 的正整数,都有
的正整数,都有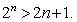
证法2:当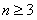 时
时
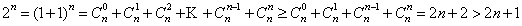
综上所述,当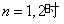
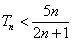 ,当
,当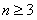 时
时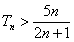
……………………14分
21、解:函数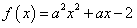 在
在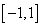 上存在零点
上存在零点
∴方程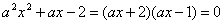 有解
有解
显然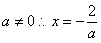 或
或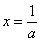 ……………………………………2分
……………………………………2分
∵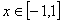 ,故
,故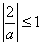 或
或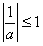
∴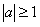 ……………………………………4分
……………………………………4分
只有一个实数满足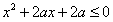 即抛物线
即抛物线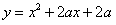 与x轴只有一个交点
与x轴只有一个交点
∴ 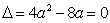
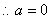 或
或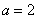 ……………………………………8分
……………………………………8分
∴命题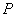 或
或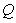 为真命题时,
为真命题时,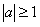 或
或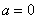
∵命题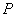 或
或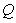 为假命题
为假命题
∴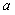 的取值范围为
的取值范围为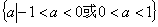 ……………………………………12分
……………………………………12分
20、解:设楼房每平方米的平均综合费用为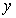 元,依题意得
元,依题意得
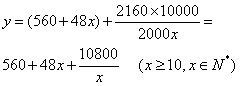 .……………… 4分
.……………… 4分
解法1: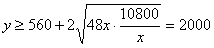 ……………… 8分
……………… 8分
当且仅当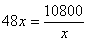 ,即x=15时,“=”成立。
,即x=15时,“=”成立。
因此,当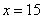 时,
时,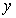 取得最小值,
取得最小值,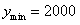 元.………………12分
元.………………12分
解法2: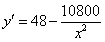 ,令
,令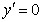 ,即
,即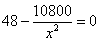 ,解得
,解得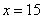
当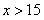 时,
时,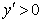 ;当
;当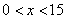 时,
时,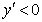 ,
,
因此,当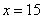 时,
时,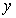 取得最小值,
取得最小值,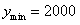 元.
元.
答:为了使楼房每平方米的平均综合费最少,该楼房应建为15层。
19、解:(I)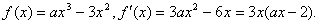 .………………2分
.………………2分
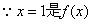 的一个极值点,
的一个极值点,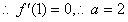 ; ………………6分
; ………………6分
(II)①当a=0时, 在区间(-1,0)上是增函数,
在区间(-1,0)上是增函数, 符合题意;
符合题意;
②当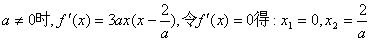 ;
;
当a>0时,对任意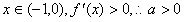 符合题意;
符合题意;
当a<0时,当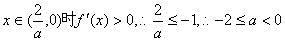 符合题意;
符合题意;
综上所述,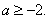 ……………………………………………12分
……………………………………………12分
18、解:(Ⅰ)设该射手第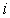 次击中目标的事件为
次击中目标的事件为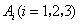 ,则
,则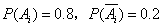 ,
,
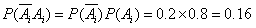 .
4分
.
4分
(Ⅱ)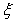 可能取的值为0,1,2,3.
可能取的值为0,1,2,3.
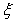 的分布列为
的分布列为
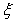 |
0 |
1 |
2 |
3 |
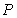 |
0.008 |
0.032 |
0.16 |
0.8 |
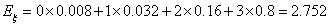 12分
12分
17、解:(I)因为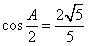 ,
,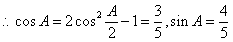 ,又由
,又由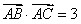 ,得
,得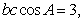
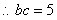 ,
,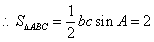 6分
6分
(II)对于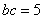 ,又
,又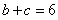 ,
, 或
或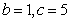 ,由余弦定理得
,由余弦定理得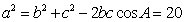 ,
,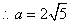 21世纪教育网 12分
21世纪教育网 12分
13. 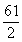 14.
14. 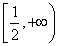 15.
15. 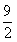 16.
16. 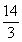
1.C 2.D 3.B 4.C 5.C 6.C 7.A 8.B 9.A 10.D 11.B12.A
22、已知数列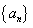 的前n项和
的前n项和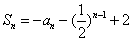 (n为正整数)。
(n为正整数)。
(Ⅰ)令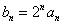 ,求证数列
,求证数列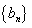 是等差数列,并求数列
是等差数列,并求数列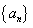 的通项公式;
的通项公式;
(Ⅱ)令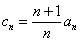 ,
,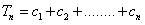 比较
比较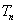 与
与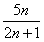 的大小,并证明。(本小题满分14分)
的大小,并证明。(本小题满分14分)
答案 及 评 分 标 准
21、已知命题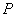 :“函数
:“函数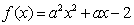 在
在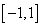 上存在零点”;
命题
上存在零点”;
命题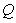 :“只有一个实数
:“只有一个实数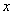 满足不等式
满足不等式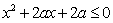 ”;若命题
”;若命题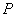 或
或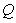 是假命题,求实数
是假命题,求实数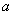 的取值范围.(本题满分12分)
的取值范围.(本题满分12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com