
21.求下列函数的值域(6分)
(1) (2)
(2)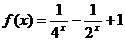 ,
,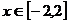 )
)
20.已知:
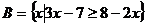 ,求
,求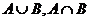 .(6分)
.(6分)
19.对于函数 定义域中任意的
定义域中任意的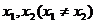 ,有如下结论:
,有如下结论:
①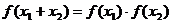 ; ②
; ②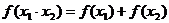 ;
;
③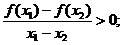 ④
④
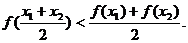
当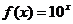 时,上述结论中正确结论的序号是________________
时,上述结论中正确结论的序号是________________
18.已知函数 则不等式
则不等式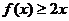 的解集为__________________.
的解集为__________________.
17.若函数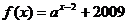 (
( 为大于1的任意实数)恒过一定点,此定点为________.
为大于1的任意实数)恒过一定点,此定点为________.
16.函数 在区间
在区间 上是减函数,则
上是减函数,则 的取值范围是__________________.
的取值范围是__________________.
14.已知幂函数 的图象经过点
的图象经过点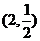 ,则
,则 __________ . .
__________ . .
15. ________.
________.
13.某班有学生55人,其中音乐爱好者35人,体育爱好者45人,还有4人既不爱好体育也不爱好音乐,则班级中即爱好体育又爱好音乐的有__________ 人.
17.解:由已知,得 …………2分
…………2分
(1)最小正周期 .
…………4分
.
…………4分
(2)令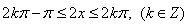 …………6分
…………6分
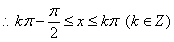 …………7分
…………7分
又 ,
,
 或
或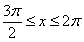 , …………9分
, …………9分
所以原函数的单调递增区间为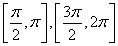 .
…………10分
.
…………10分
18解: 等差数列
等差数列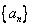 的前
的前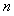 和为
和为
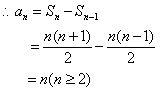 …………2分
…………2分
又当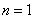 时,
时,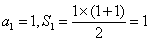 ,
,
 数列
数列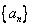 的通项公式为
的通项公式为 ………… 3分
………… 3分
由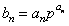 ,得
,得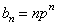 .
.
所以 ,
…………4分
,
…………4分
当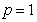 时,
时,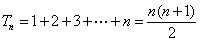 ;
…………5分
;
…………5分
当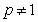 时,
时,
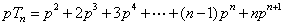 , …………7分
, …………7分
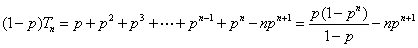 …9分
…9分
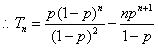 …………10分
…………10分
综上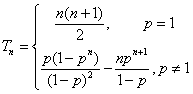 .
…………12分
.
…………12分
19解:(1)由 ………1分
………1分
 ………3分
………3分
又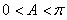
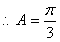 ………5分
………5分
(2)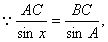
 ………6分
………6分
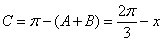 ,
,
同理: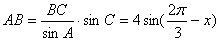 ………7分
………7分
 ………9分
………9分

 ………10分
………10分
故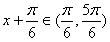 ,
, ,
,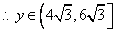 . ………12分
. ………12分
20解:(1)由题得 .
.

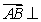
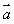 ,
,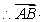
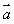
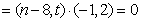 ,
……….2分
,
……….2分
得 ,则
,则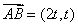 .
.
又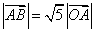 ,
,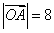 .
.
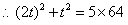 ,解得
,解得 .
………4分
.
………4分
当 时,
时,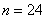 ;当
;当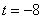 时,
时,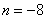 .
.
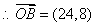 或
或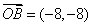 .
………6分
.
………6分
(2)由已知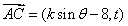
 向量
向量 与向量
与向量 共线,
共线,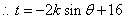 , ………7分
, ………7分
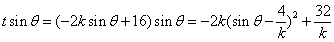 .
.
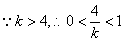 ,
………8分
,
………8分
故当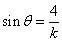 时,
时,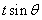 取最大值
取最大值 时,有
时,有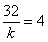 ,得
,得 .
………10分
.
………10分
这时,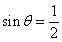 ,且
,且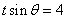 ,得
,得 ,则
,则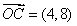 . ………11分
. ………11分
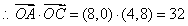 .
………12分
.
………12分
21解:(1)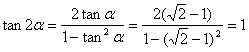 ………1 分
………1 分
又∵ 为锐角,∴
为锐角,∴ ………2分
………2分
∴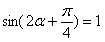
 ………3分
………3分
(2)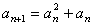 ∵
∵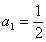 ∴
∴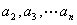 都大于0
都大于0
∴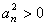 ∴
∴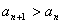 ………5分
………5分
(3) 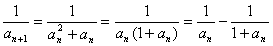
∴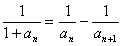 ………7分
………7分
∴
 ………9分
………9分
 ………10分
………10分
∵ ,
,  ,
,
又∵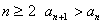 ∴
∴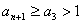 ∴
∴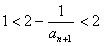
∴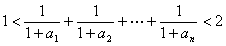 ………12分
………12分
22解:(1)由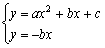 ,消去
,消去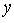 ,得
,得 , ………1分
, ………1分

 ………2分
………2分

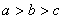 ,
,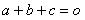
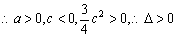 两函数的图象交于不同的两点
两函数的图象交于不同的两点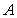 、
、 ………4分
………4分
(2)法一:
由已知 ,即为
,即为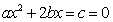 ………5分
………5分
由(1)知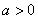 且上述方程一定有两不等实根
且上述方程一定有两不等实根
 ………6分
………6分
记 ,
,
则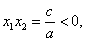
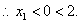 ………7分
………7分
又
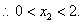 ………8分
………8分
综上,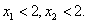
法二:
 的两根为
的两根为
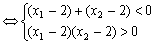 而
而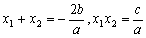
于是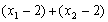
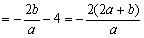

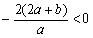
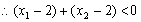 ,
,
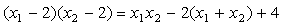
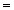

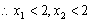
(3)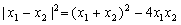
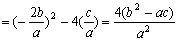
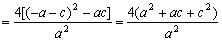
 ………9分
………9分
由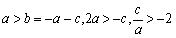 由
由 ………10分
………10分
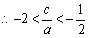 ,则
,则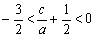 故
故
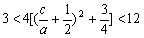 ,
,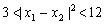 ………11分
………11分
又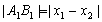 ,故
,故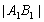 的取值范围为
的取值范围为 ………12分
………12分
13.9
14.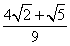 15.4018 16.① ③ ⑤
15.4018 16.① ③ ⑤
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com