3．目前对化合物种类最多的族和元素种类最多的族的说法，你认为正确的是

A．分别是IVA和IA族　　　　 B．分别是VIA族和IA族

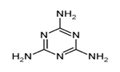C．分别是IVA和IIIB族　 　　　D．分别是VIA族和IIIB族

2．下列关于科学家及相关事实错误的是

　　 A．德国维勒：第一次用无机物合成有机物　 B．瑞典贝采利乌斯：提出有机化学概念

C．德国李比希：提出基团理论　　 　　D．美国科里：运用同位素示踪法研究反应历程

1．北京奥运会火炬使用的燃料是一种常用燃料，其分子式为C₃H₈，它属于

A．烷烃　 　　　　B．烯烃　　　　　 C．炔烃　　　　 　D．芳香烃

23.(本题满分10分)选修4-1几何证明选讲

从圆外一点向圆引两条切线(为切点)和割线(与圆交于两点).从点作弦平行于，连接交于.连接.求证：.

证明：又 是圆的两条切线，

22.(本题满分10分)选修4-5不等式选讲

已知函数，其中，若不等式对任意恒成立，求实数的取值范围.

解：

只需即

21．(本题满分12分)

已知点都在直线：上，为直线与轴的交点，数列成等差数列，

公差为1.()

(1)求数列，的通项公式；

(2)若= ，问是否存在,使得成立；若存在，求出的值，若不存在，说明理由.

解：(1)，

　　　　 ，

(2)不存在这样的

　　 假设存在

①若为奇数，则

　　　　 所以无解

②若为偶数，则

所以，解得矛盾

请考生在第22,23两题中任选一题做答，写出必要解答过程，如果多做，则按所做的第一题计分

20．(本题满分12分)

设椭圆E: 过两点，为坐标原点，

(1)求椭圆E的方程；

(2)若存在圆心在原点的圆，使得该圆的任意一条斜率存在的切线与椭圆恒有两个交点,且？求出该圆的方程.

解:(1)因为椭圆E: (a,b>0)过M(2，) ，N(,1)两点,

所以解得所以椭圆E的方程为

(2)设斜率为，则该圆的切线方程为解方程组得,即, 　 　

则△=,即

_，

要使,需使,即,所以,

所以又,所以,所以,即或,因为直线为圆心在原点的圆的一条切线,所以圆的半径为,,,所求的圆为

19.(本题满分12分)

设函数，其中常数

(1)讨论的单调性；(2)若方程在时有唯一解，求实数的取值　　

解：(1)

令得

增区间是和；减区间是

(2)由(1)知在和均递增，且

时，

解法一：①若，即亦即时，

则在上连续单调，且，所以方程在内有一个实根，又由表达式知存在一个充分大的正数X，使X且，由零点存在性定理知，在内至少有一实根与在内存在唯一实根矛盾.

②若，则对一切均有，故方程在无实根.

③若，即时，则是在内的唯一实根

解法二：又，要使方程在时有唯一解，只需，即

综上，的值为6

18．(本题满分12分)

在四棱锥中，底面边长为，侧棱长为，为侧棱上的一点

(1)当四面体的体积为时，求的值；

(2)在(1)的条件下，若是的中点，

求证：

解：(1)设，设作于，且为交线，

则，又

在中，

解得：

(2)取中点，连结，

则

则

而为平面内的两条相交直线，

而，

17．(本题满分12分)

已知是等比数列的前项和，成等差数列，求证：成等差数列.

证明：成等差数列，公比，，

　　　 ， 得证.