
16.(本小题满分12分)
己知向量a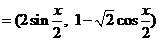 ,b
,b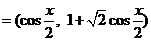 ,函数
,函数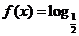 (a·b).
(a·b).
(Ⅰ)求函数f(x)的定义域和值域;
(Ⅱ)求函数f(x)的单调区间.
[解](Ⅰ)因为a·b=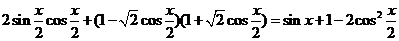
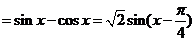 .
(2分)
.
(2分)
由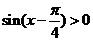 ,得
,得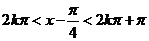 ,即
,即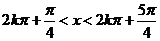 ,k∈Z.
,k∈Z.
所以f(x)的定义域是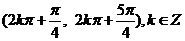 .
(4分)
.
(4分)
因为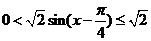 ,则
,则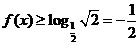 ,
,
所以f(x)的值域是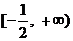 .
(6分)
.
(6分)
(Ⅱ)由题设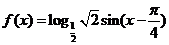 .
.
若f(x)为增函数,则 为减函数,所以
为减函数,所以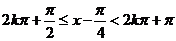 ,即
,即
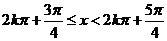 ,故f(x)的递增区间是
,故f(x)的递增区间是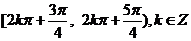 . (9分)
. (9分)
若f(x)为减函数,则 为增函数,所以
为增函数,所以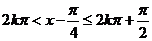 ,即
,即
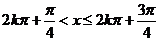 ,故f(x)的递减区间是
,故f(x)的递减区间是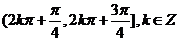 . (12分)
. (12分)
15.设直角三角形的两直角边的长分别为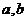 ,斜边长为
,斜边长为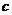 ,斜边上的高为
,斜边上的高为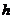 ,则有
,则有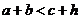 成立,某同学通过类比得到如下四个结论:
成立,某同学通过类比得到如下四个结论:
①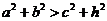 ;②
;②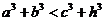 ;③
;③ 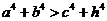 ;④
;④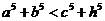 .
.
其中正确结论的序号是 ②
④ ;进一步类比得到的一般结论是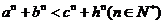 .
.
[解析]在直角三角形ABC中,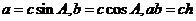 ,所以
,所以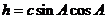 .
.
于是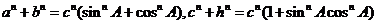 .
.
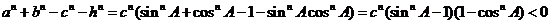 .
.
所以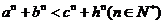 .
.
14.已知函数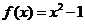 ,集合M=
,集合M= ,N=
,N=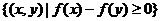 ,则集合
,则集合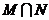 所表示的平面区域的面积是
π .
所表示的平面区域的面积是
π .
[解析]因为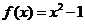 ,
,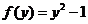 ,则
,则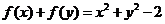 ,
,
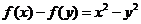 .所以
.所以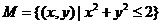 ,
,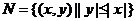 .
.
故集合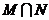 所表示的平面区域为两个扇形,其面积为圆面积的一半,即为π.
所表示的平面区域为两个扇形,其面积为圆面积的一半,即为π.
13. 2009年北京国庆阅兵式上举行升旗仪式,如图,在坡度为15°的观礼台上,某一列座位与旗杆在同一个垂直于地面的平面上,在该列的第一排和最后一排测得旗杆顶端的仰角分别为60°和30°,且第一排和最后一排的距离为
2009年北京国庆阅兵式上举行升旗仪式,如图,在坡度为15°的观礼台上,某一列座位与旗杆在同一个垂直于地面的平面上,在该列的第一排和最后一排测得旗杆顶端的仰角分别为60°和30°,且第一排和最后一排的距离为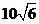 米,则旗杆的高度为 30 米 .
米,则旗杆的高度为 30 米 .
[解析]设旗杆高为h米,最后一排为点A,
第一排为点B,旗杆顶端为点C,则
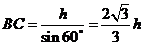 .
.
在△ABC中,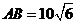 ,∠CAB=45°,∠ABC=105°,
,∠CAB=45°,∠ABC=105°,
所以∠ACB=30°,由正弦定理得,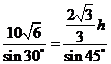 ,故
,故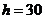 .
.
12.已知函数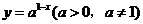 的图象恒过定点A,若点A在直线
的图象恒过定点A,若点A在直线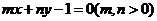 上,则
上,则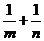 的最小值为 4
.
的最小值为 4
.
[解析]显然函数图象过定点(1,1),由已知,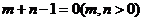 ,即
,即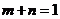 .
.
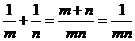 .又
.又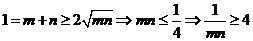 ,故最小值为4.
,故最小值为4.
11.已知曲线C的参数方程为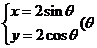 为参数),直线
为参数),直线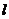 的极坐标方程为
的极坐标方程为
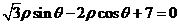 ,设点A为曲线C上任意一点,点B为直线
,设点A为曲线C上任意一点,点B为直线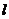 上任意一点,则
上任意一点,则
A,B两点间的距离的最大值是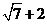 .
.
[解析]曲线C的普通方程为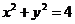 ,直线
,直线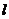 的直角坐标方程为
的直角坐标方程为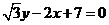 .
.
所以|AB|的最大值为圆心到直线的距离加上圆的半径,即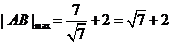 .
.
10.已知函数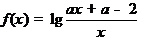 在区间[1,2]上是增函数,则实数a的取值范围是(1,2).
在区间[1,2]上是增函数,则实数a的取值范围是(1,2).
[解析]因为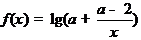 在区间[1,2]上是增函数,所以
在区间[1,2]上是增函数,所以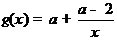 在区间[1,2]上是增函数,且
在区间[1,2]上是增函数,且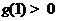 .于是
.于是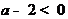 ,且
,且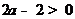 ,即
,即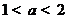 .
.
9.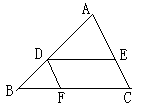 如图,在△ABC中,DE∥BC,DF∥AC,AE︰AC=3︰5,
如图,在△ABC中,DE∥BC,DF∥AC,AE︰AC=3︰5,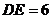 ,则BF=__4__.
,则BF=__4__.
[解析]因为DE∥BC,则△ADE-△ABC,
所以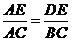 ,即
,即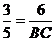 ,所以
,所以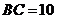 .
.
又DF∥AC,则四边形DECF是平行四边形,
故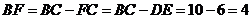 .
.
8.对于向量a,b,定义a×b为向量a,b的向量积,其运算
结果为一个向量,且规定a×b的模|a×b|=|a||b|sinθ(其中
θ为向量a与b的夹角),a×b的方向与向量a,b的方向都
垂直,且使得a,b,a×b依次构成右手系.如图,在平行六
面体ABCD-EFGH中,∠EAB=∠EAD=∠BAD=60°,
AB=AD=AE=2,则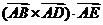 =
( D )
=
( D )
A. 4
B. 8 C.
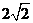 D.
D.
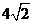
[解析]据向量积定义知,向量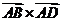 垂直平面ABCD,且方向向上,设
垂直平面ABCD,且方向向上,设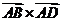 与
与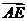 所成角为θ.
所成角为θ.
因为∠EAB=∠EAD=∠BAD=60°,所以点E在底面ABCD上的射影在直线AC上.
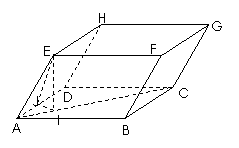 作EI⊥AC于I,则EI⊥面ABCD,所以θ+∠EAI=
作EI⊥AC于I,则EI⊥面ABCD,所以θ+∠EAI=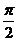 .
.
过I作IJ⊥AD于J,连EJ,由三垂线逆定理可得EJ⊥AD.
因为AE=2,∠EAD=60°,所以AJ=1,EJ=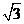 .
.
又∠CAD=30°,IJ⊥AD,所以AI=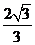 .
.
因为AE=2,EI⊥AC,所以cos∠EAI=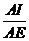 =
=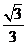 .
.
所以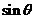 =
=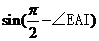 =cos∠EAI=
=cos∠EAI=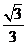 ,
,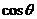 =
=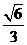 .
.
故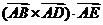 =|
=|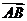 ||
||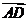 |sin∠BAD|
|sin∠BAD|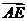 |
|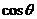 =8×
=8×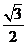 ×
×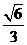 =
=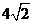 ,故选D.
,故选D.
7.设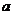 为函数
为函数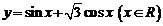 的最大值,则二项式
的最大值,则二项式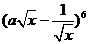 的展开式中含
的展开式中含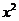 项的系数是
( C )
项的系数是
( C )
A.192
B.182
C.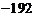 D.
D.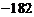
[解析]因为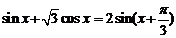 ,由题设
,由题设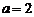 .
.
则二项展开式的通项公式为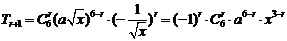 .
.
 令3-r=2,得
令3-r=2,得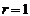 .所以含
.所以含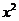 项的系数是
项的系数是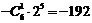 ,故选C.
,故选C.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com