18、解：(Ⅰ)设该射手第次击中目标的事件为，则，

．　　　　　　　　　 4分

(Ⅱ)可能取的值为0，1，2，3．　　

的分布列为

	0	1	2	3
	0.008	0.032	0.16	0.8

　　　　　　　　　 12分

17、解：(I)因为，，又由，得，　　　　　　　　　 6分

(II)对于，又，或，由余弦定理得， 21世纪教育网　 　　　　　　　　　　12分

13. 　　14.　 　　15.　 　16.

1.C 2.D 3.B　 4.C　 5.C　 6.C　 7.A　 8.B　 9.A 10.D 11.B12.A

22、已知数列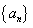的前n项和(n为正整数)。

(Ⅰ)令，求证数列是等差数列，并求数列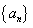的通项公式；

(Ⅱ)令，比较与的大小，并证明。(本小题满分14分)

答案 及 评 分 标 准

21、已知命题：“函数在上存在零点”；　 命题：“只有一个实数满足不等式”；若命题或是假命题，求实数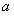的取值范围．(本题满分12分)

20、某单位用2160万元购得一块空地，计划在该地块上建造一栋至少10层、每层2000平方米的楼房。经测算，如果将楼房建为x(x10)层，则每平方米的 平均建筑费用为560+48x(单位：元)。为了使楼房每平方米的平均综合费用最少，该楼房应建为多少层？(注：平均综合费用=平均建筑费用+平均购地费用，平均购地费用=)

(本题满分12分)

19、已知定义在R上的函数，其中a为常数.　

(I)若x=1是函数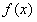的一个极值点，求a的值；

　 (II)若函数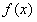在区间(－1，0)上是增函数，求a的取值范围；(本题满分12分)

18．某射击测试规则为：每人最多射击3次，击中目标即终止射击，第次击中目标得分，3次均未击中目标得0分．已知某射手每次击中目标的概率为0.8，其各次射击结果互不影响．

(Ⅰ)求该射手恰好射击两次的概率；

(Ⅱ)该射手的得分记为，求随机变量的分布列及数学期望．(本题满分12分)

17、在中，角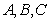所对的边分别为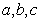，且满足，

　　 ．(I)求的面积；(II)若，求的值．(本题满分12分)