4．普通小麦中有高秆抗病(TTRR)和矮秆易感病(ttrr)两个品种，控制两对性状的基因分别位于两对同源染色体上。实验小组利用不同的方法进行了如下三组实验：

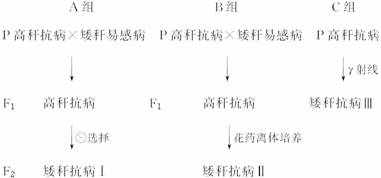
下列关于该实验的说法，除哪项外，其余都是正确的

A．A组、B组和C组所运用的育种方法分别是杂交育种、单倍体育种和诱变育种

B．A组和B组都利用杂交的方法，目的是一致的

C．F₂中的矮秆抗病植株可以直接用于生产

D．C组r射线要处理萌发的种子或幼苗

答案　C

3．(2009·江西六校联考)人体的糖蛋白必须经内质网和高尔基体进一步加工合成。通过转基因技术，可以使人的糖蛋白基因得以表达的受体细胞是

A．大肠杆菌　 　　　　　　　　　　　　　　　　　　　　　　　 B．酵母菌

C．噬菌体　 　　　　　　　　　　　　　　　　　　　　　　　　　 D．质粒DNA

解析　噬菌体和质粒都没有细胞结构，显然不合题意。大肠杆菌是原核细胞，不含内质网和高尔基体，也不能作为受体细胞。酵母菌是真核生物，细胞内含有内质网和高尔基体可以满足要求。

答案　B

2．下列各种育种措施中，能产生新基因的是

A．高秆抗锈病小麦和矮秆易染锈病小麦杂交获矮秆抗锈病优良品种

B．用秋水仙素诱导二倍体西瓜获得无子西瓜

C．用X射线、紫外线处理青霉菌获得高产青霉株

D．用离体花药培育小麦植株

解析　人工诱变育种能产生新基因，选C。

答案　C

1．一旦禽流感病毒与人类病毒重组，从理论上讲，就有可能在人与人之间传播该疾病。届时，这种病毒就会成为人类病毒。这里所说的重组与下列哪项本质相同

A．基因工程　　　　　　　　 　B．太空育种

C．单倍体育种　 　　　　　　　　　　　　　　　　　　　　　 D．多倍体育种

解析　不同类型的病毒重组实质是病毒间的基因转移和拼接，与基因工程本质是相同的，都是基因重组，只是基因工程是人为操作的，病毒之间的基因重组是自发的。

答案　A

5.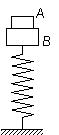5、竖直放置的轻弹簧，上端与质量为3kg的物块B相连接。另一个质量为1kg的物块A 放在B上。先向下压A，然后释放，A、B共同向上运动一段路程后将分离。分离后A又上升了0.2m到达最高点，此时B的速度方向向下，且弹簧恰好为原长。则从A、B分离到A上升到最高点过程中，弹簧弹力对B做功的大小及弹簧回到原长时B的速度大小。(取g=10m/s²)

A．12J，2m/s　　　　　　　　　　　　　　　　　　　　　 B．0，2m/s

C．0，0　　　　　　　　　　　　　　　　　　 　　　　D．4J，2m/s

5、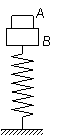如图所示，A、B两木块叠放在竖直轻弹簧上，已知木块A、B质量分别为0.42kg和0.40kg，弹簧的劲度系数k=100N/m，若在木块A上作用一个竖直向上的力F，使A由静止开始以0.5m/s²的加速度竖直向上做匀加速运动(g=10m/s²)。求：

(1)使木块A竖直做匀加速度运动的过程中，力F的最大值；

(2)若木块由静止开始做匀加速运动，直到A、B分离的过程中，弹簧的弹性势能减少了0.248J，求这一过程中F对木块做的功。

［解析］此题难点在于能否确定两物体分离临界点。

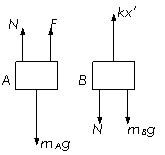当F=0(即不加竖直向上F力)时，设木块A、B叠放在弹簧上处于平衡时弹簧原压缩量为x，有

kx=(m_A+m_B)g　　 ①

即　　　

对于木块A施加力F，A、B受力如图所示。

对木块A有

F+N–m_Ag= m_Aa，　　　 ②

对于木块B有

kx′–N–m_Bg= m_Ba。　　　　 ③

可知，当N≠0时，A、B加速度相同，由②式知欲使木块A匀加速度运动，随N减小F增大。当N=0时，F取得了最大值F_m，

即：F_m=m_A(g+a)=4.41N。

又当N=0时，A、B开开始分离，由③式知，弹簧压缩量kx′=m_B(a+g)，

则：　　　　　　　　　　　　　　　　　　　　　　　 ④

木块A、B的共同速度　　　　　　　 　　 　　　 ⑤

由题知：此过程弹性势能减少了E_p=0.248J。

设F力所做的功为W_F，对这一过程应用功能原理，得：

　 ⑥

联立①④⑤⑥式，得W_F=9.64×10^–2J。

4.4、如图所示，在粗糙水平桌面上放有A、B两个物体，A、B间用一根轻质硬杆C 相连，已知物体A的质量是m₁＝5kg，B的质量是m₂＝3kg。A与桌面的动摩擦因数是μ₁=0.2，B与桌面间的动摩擦因数是μ₂=0.5。现在A上施加水平向右的拉力F，使它们以v=10m/s的速度沿水平面向右匀速运动。g取10m/s²，求：

(1)水平向右的拉力F的大小及轻杆C上的弹力大小；

(2)若在某时刻突然撤去拉力F，则A、B在水平面上滑动的距离是多大？

(1)25N，15N　　 (2)16m

题型五：弹簧变化过程中运动分析

解决这类问题需要注意： 弹簧的弹力是一种由形变决定大小和方向的力，注意弹力的大小与方向时刻要与当时的形变相对应。一般应从弹簧的形变分析入手，先确定弹簧原长位置、现长位置及临界位置，找出形变量x与物体空间位置变的几何关系，分析形变所对应的弹力大小、方向，弹性势能也是与原长位置对应的形变量相关。从此来分析计算物体运动状态的可能变化。

通过弹簧相联系的物体，有运动过程中经常涉及临界极值问题：如物体的速度达到最大；弹簧形变量达到最大；使物体恰好离开地面；相互接触的物体恰好脱离等。此类问题的解题关键是利用好临界条件，得到解题有用的物理量和结论。

4、如图所示，一辆汽车A拉着装有集装箱的拖车B，以速度v₁＝30 m/s进入向下倾斜的直车道。车道每100 m下降2 m。为了使汽车速度在s＝200 m的距离内减到v₂＝10 m/s，驾驶员必须刹车。假定刹车时地面的摩擦阻力是恒力，且该力的70%作用于拖车B，30%作用于汽车A。已知A的质量m₁＝2000 kg，B的质量m₂＝6000 kg。求汽车与拖车的连接处沿运动方向的相互作用力。取重力加速度g＝10 m/s²。

　 ［解析］

汽车沿倾斜车道作匀减速运动，有：

用F表示刹车时的阻力，根据牛顿第二定律得：

式中：

设刹车过程中地面作用于汽车的阻力为f，依题意得：

用f_N表示拖车作用汽车的力，对汽车应用牛顿第二定律得：

联立以上各式解得：　　　　 f_N = 880N

3.3、放在水平面上的物块，受到方向不变水平推力F的作用，F与时间t的关系和物块速度v与时间t的关系如图所示，取重力加速度g=10 m/s²。由此两图线可以求得物块的质量m和物块与地面之间的动摩擦因数μ分别为

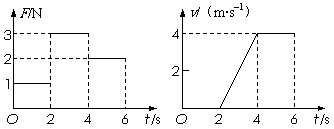A．m=0.5kg，μ=0.4

B．m=1.5kg，μ=

C．m=0.5kg，μ=0.2

D．m=1kg，μ=0.2

题型四：连接体问题

解决这类问题需要注意：若连接体内(即系统内)各物体具有相同的加速度时，应先把连接体当成一个整体(即看成一个质点)，分析其受到的外力及运动情况，利用牛顿第二定律求出加速度．若连接体内各物体间有相互作用的内力，则把物体隔离，对某个物体单独进行受力分析(注意标明加速度的方向)，再利用牛顿第二定律对该物体列式求解。

3、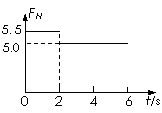固定光滑细杆与地面成一定倾角，在杆上套有一个光滑小环，小环在沿杆方向的推力F作用下向上运动，推力F与小环速度v随时间变化规律如图所示，取重力加速度g＝10m/s²。求：

(1)小环的质量m；

(2)细杆与地面间的倾角a。

　 ［解析］

(1)前2s： 　　　　 ①　　　　

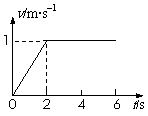由v-t图象可知

2s以后：　　　　　　 　　 ②

由①②得：

(2)由②式，所以a=30°。