7. 一般人造地球卫星

例7：以第一宇宙速度运行的卫星也称为近地卫星，如果卫星离地面高度为几十甚至上百公里，相对于地球半径公里为小量，这些卫星都可看成近地卫星。已知地面上重力加速度，求第一宇宙速度。如有一颗卫星，质量，以绕地球做匀速圆周运动，由于受太空尘埃的影响，其运行轨道高度下降1公里，求其下降前后重力势能的改变量(保留二位有效数字)。

解：万有引力提供向心力：

又近地面物体

位置的重力加速度为

，

即有，即

所以重力势能减少量：

6. 关于双星问题

例6：宇宙中两颗相距较近的天体称为“双星”，它们以二者连线上的某点为圆心做匀速圆周运动，而不至于因万有引力的作用吸引到一起，如图2所示，设二者的质量分别为和，二者相距。

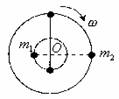
图2

(1)证它们的轨道半径之比、线速度之比都等于质量的反比；

(2)试写出它们角速度的表达式。

证明：

(1)双星间的万有引力提供各自的向心力，由万有引力定律

　 得，

(2)由，，

得

5. 关于地球自转问题

例5：有一种说法广为流传，那就是“坐地日行八万里”，试用你所学的物理知识来解释一下这句话是否有道理。

解：这句话有一定的科学道理。

由于地球在围绕太阳公转的同时还在不停地绕地轴自转，对于地面上的人而言将随着地球一起绕地轴做圆周运动，一日内刚好绕地轴运动一周，相应的长度为圆周的周长，以赤道上的人为例，有

所以里里

若离开赤道，很显然相应的长度会变小。

4. 求行星的自转周期

例4：某球形行星“一昼夜”时间为T=6h，在该行星上用弹簧秤称同一物体的质量，发现其“赤道”上的读数比其在“南极”处读数小9%，若设想该行星的自转速度加快，在其“赤道”上的物体会自动“漂浮”起来，这时该行星的自转周期多大？

解：由万有引力定律，可得

在南极：

在赤道：

又，代入数据

3. 求中子星表面的重力加速度及第一宇宙速度　

例3：某中子星的质量大约与太阳的质量相等为。但是它的半径为10km，已知万有引力常量，求：

(1)此中子星表面的重力加速度。

(2)贴近中子星的表面，沿圆轨道运动的小卫星的速度。

解：

(1)设中子星表面的重力加速度为

在中子星表面：

(2)贴近中子星表面，小卫星的轨道半径

由万有引力提供向心力，得

得

2. 估算地球的质量

例2：某同学根据当地的重力加速度值，地球半径6370km，估算出地球质量，试问他是怎样估算的(万有引力恒量为，保留二位有效数字)？

解：该同学是根据地球表面重力近似等于万有引力来估算的。

由得

自然界中任何两个物体都是相互吸引的，引力的大小跟这两个物体的质量的乘积成正比，跟它们的距离的二次方成反比，表达式是。设天体和卫星的运动是匀速圆周运动，那么万有引力提供其做圆周运动的向心力，即有

。应用万有引力定律，可以解决有关天文和地球卫星问题。

1. 估算太阳的平均密度

例1：利用万有引力定律、小孔成像原理和生活常识，就可以估算出太阳的平均密度。用长L=80cm的不透光圆筒，在其一端封上厚纸，纸的中间用针扎一个直径0.5mm左右的小孔，筒的另一端封上一张白纸，把有小孔的一端对准太阳，在另一端可看到太阳的像。如图1所示，若测得太阳的像的直径为，试估算太阳的平均密度(保留二位有效数字)。

图1

解：设太阳半径为R，地日距离为，OA距离为D，由相似三角形可得：

又，故

设太阳、地球质量分别为M、，地球绕日周期为T

万有引力提供向心力：

又，所以

代入数据：

2. 利用黄金代换，架起“天”与“地”的桥梁

例4：已知地球的半径为，又知月球绕地球的运动可近似看作匀速圆周运动，则可估算从月球到地心的距离为　　　　 m。(结果保留一位有效数字)

解析：设月球到地心的距离为，由万有引力提供向心力有

　①

月球绕地球的公转周期为T=27.3d

在地球表面万有引力提供重力则 ②

其中M为地球的质量，R为地球的半径，为地球表面的重力加速度取

由①②得

例5：2002年3月25日，我国自行研制的新型“长征”运载火箭，将模拟载人航天试验飞船“神州3号”送入预定轨道，飞船绕地球遨游太空后又顺利返回。飞船在运动过程中进行了预定的空间科学实验，获得圆满成功。设飞船轨道离地高度为，地面重力加速度，地球半径为，则“神舟3号”飞船绕地球正常运转多少圈？

解析：飞船运行，要求飞船绕地球正常运转的圈数，只需求出飞船在离地高度时飞行的周期，由万有引力提供向心力则

　①

其中

在地球表面万有引力提供重力，则有，所以 ②

由①②得

则飞船环绕地球正常运转的圈数

代入数据得圈

1. 有关同一物体在不同星体表面重力加速度的计算

　　 (1)比较两不同星体表面的重力加速度

例1：一卫星绕某行星做圆周运动，已知行星表面的重力加速度为，行星的质量与卫星的质量之比，行星的半径与卫星的半径之比，行星与卫星之间的距离与行星的半径之比。设卫星表面的重力加速度为，则在卫星的表面有。经计算得出：卫星表面的重力加速度为行星表面的重力加速度的三千六百分之一。上述结论是否成立？说明理由。

解析：看结论是否正确，只需求出卫星表面的重力加速度与行星表面的重力加速度之比。紧紧抓住万有引力提供重力，则

在卫星表面的物体：

在行星表面的物体：

所以其重力加速度之比为

即结论不对。

其比值应为。

(2)与平抛运动联系求水平射程

例2：某星球的质量约为地球质量的9倍，半径约为地球半径的，若在地球上高处平抛一物体，水平射程为60m，则在该星球上从同样高度以同样的初速度平抛同一物体，水平射程为多少？

解析：由平抛运动知识知，水平射程取决于竖直方向的时间和初速度。当从同样高度以同样的初速度在不同的星体表面平抛同一物体，由于不同星体表面的重力加速度不同，因而下落同样的高度所用的时间不同，即以同样的初速度抛出时，水平射程不同。故此题转化为求星球和地球表面的重力加速度之比。

在星球表面的物体：

在地球表面的物体：

则加速度之比为：

平抛物体时，

所以。

则水平射程之比为

星球表面的水平射程

(3)与竖直上抛运动联系求最大高度

例3：已知月球质量是地球质量的，月球的半径是地球半径的，那么在月球和地球表面附近，以同样的初速度分别竖直上抛一个物体时，忽略空气阻力，上升的最大高度之比是多少？

解析：在忽略空气阻力的情形下，上升的高度与初速度的关系为，当以同样的初速度分别竖直上抛一个物体时，高度与加速度成反比。

设月球的质量、半径和表面的重力加速度分别为、、；地球的质量、半径和表面的重力加速度分别为、、，由万有引力提供重力得

，

于是上升的最大高度之比为

应用万有引力定律解决有关天体运动问题时，往往要涉及到牛顿运动定律和圆周运动的知识，是较为典型的力学综合，解决问题过程较为繁琐，且易出错。如果我们能掌握一些推论并能灵活运用，将会化繁化简，变难为易，解决问题的思路和方法清晰明了，方便快捷。下面浅谈一孔之见，与大家共同商讨。

题型一：--关系

在质量为M的某天体上空，有一质量为的物体，距该天体中心的距离为，所受重力为万有引力：

由上式可得常量或

推论一：在某天体上空物体的重力加速度与成反比。即

或 ①

例1：设地球表面重力加速度为，物体在距离地心4R(R是地球的半径)处，由于地球的作用而产生的重力加速度为，则为(　　 )

A. 1　　 B. 　　C. 　　D.

解析：由①式得

答案应选D。

题型二：--关系

有一质量为的物体(卫星或行星等)绕质量为M的天体做匀速圆周运动，其轨道半径为，线速度为，万有引力提供向心力：

由上式可得常量或

推论二：绕某天体运动物体的速度与轨道半径的平方根成反比。即

或 ②

例2：已知人造地球卫星靠近地面运行时的环绕速度约为，则在离地面的高度等于地球半径处运行的速度为(　　 )

A. 　　B. 　　C. 　　D.

解析：由②式得

答案应选C

题型三：--关系

有一质量为的物体(卫星或行星等)绕质量为M的天体做匀速圆周运动，其轨道半径为，角速度为，万有引力提供向心力：

由上式可得：常量或

推论三：绕某天体运动的物体的角速度的二次方与轨道半径的三次方成反比。即

或 ③

例3：两颗人造地球卫星，它们的轨道半径之比为，它们角速度之比

　　　　 。

解析：由③式可得

题型四：T--关系

有一质量为的物体(卫星或行星等)绕质量为M的天体做匀速圆周运动，其轨道半径为，周期为T，万有引力提供向心力：，

由上式可得：常量或

推论四：绕某天体运动的物体的周期T的二次方与其轨道半径的三次方成正比。即或 ④

这就是开普勒第三定律。

例4：两颗卫星在同一轨道平面绕地球做匀速圆周运动，地球半径为R，卫星距地面的高度等于R，卫星距地面的高度等于3R，则、两卫星周期之比　　　 。

解析：由④式得