22.(本小题满分14分)

已知f(x)=x³+bx²+cx+d在(－∞,0)上是增函数，在［0，2］上是减函数，且方程f(x)=0有三个根，它们分别为α,2,β.

(1)求c的值；

(2)求证：f(1)≥2;

(3)求|α－β|的取值范围.

21.(本小题满分12分)

设一次函数f(x)的图象关于直线y=x对称的图象为C，且f(－1)=0.若点(n+1,)(n∈N^*)在曲线C上，并且a₁=a₂=1.

(1)求曲线C的方程；

(2)求数列{a_n}的通项公式;

(3)设S_n=…+,求S_n.

20.(本小题满分12分)

已知双曲线=1(a>0,b>0)的左、右焦点分别为F₁、F₂，点P在双曲线的右支上，且|PF₁|=3|PF₂|.

(1)求离心率的最值，并写出此时双曲线的渐近线方程.

(2)若点P的坐标为()时，=0，求双曲线方程.

19.(本小题满分12分)

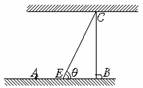
如图为河岸一段的示意图.一游泳者站在河岸的A点处，欲前往河对岸的C点处.若河宽BC为100 m，A、B相距100 m.他希望尽快到达C，准备从A步行到E(E为河岸AB上的点)，再从E游到C.已知此人步行速度为v，游泳速度为0.5v.

(1)设∠BEC=θ,试将此人按上述路线从A到C所需时间T表示为θ的函数；并求自变量θ的取值范围；

(2)θ为何值时，此人从A经E游到C所需时间T最小，其最小值是多少？

18.(本小题满分12分)

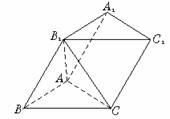
如右图所示，已知三棱柱ABC－A₁B₁C₁的各棱长均为2，侧棱B₁B与底面ABC所成的角为，且侧面ABB₁A₁垂直于底面ABC.

(1)证明AB⊥CB₁；

(2)求三棱锥B₁－ABC的体积；

(3)求二面角C－AB₁－B的大小.

17.(本小题满分12分)

袋内装有35个球，每个球上都记有从1到35的一个号码，设号码n的球重－5n+15克，这些球以等可能性从袋里取出(不受重量、号码的影响).

(1)如果任意取出1球，试求其重量大于号码数的概率；

(2)如果任意取出2球，试求它们重量相等的概率.

16.定义在R上的偶函数f(x)满足f(x+1)=－f(x)，且在［－1，0］上是增函数，给出下列关于f(x)的判断：　

①f(x)是周期函数；②f(x)关于直线x=1对称；③f(x)在［0，1］上是增函数；④f(x)在

［1，2］上是减函数；⑤f(2)=f(0),其中正确判断的序号为______(写出所有正确判断的序号).

15.在底面半径为6的圆柱内，有两个半径也为6的球面，两球的球心距为13，若作一个平面与两个球都相切，且与圆柱面相交成一椭圆，则椭圆的长轴长为______.　

14.1996年的诺贝尔化学奖授予对发现C₆₀有重大贡献的三位科学家.C₆₀是由60个C原子组成的分子，它结构为简单多面体形状.这个多面体有60个顶点，从每个顶点都引出3条棱，各面的形状分为五边形或六边形两种,则C₆₀分子中形状为五边形的面有______个，形状为六边形的面有______个.　

13.方程log₂|x|=x²－2的实根的个数为______.