
1.科学家将一段控制某药物蛋白合成的基因转移到白色来亨鸡胚胎细胞的DNA中,发育后的雌鸡就能产出含该药物蛋白的鸡蛋,在第一只鸡蛋的蛋清中都含有大量的药物蛋白;而且这些鸡蛋孵出的鸡,仍能产出含该药物蛋白的鸡蛋。以下描述不正确的是( )
A.这些鸡是转基因工程的产物 B.这种变异属于可遗传的变异
C.该过程运用了胚胎移植技术 D.该技术可定向改造生物
7、极端检验。当难以确定端点处是否成立时,可直接取其端点进行检验,以避免考虑不周全的错误。
例24、已知关于x的不等式 的解集是空集,求实数a的取值范围 。
的解集是空集,求实数a的取值范围 。
错解:由 ,解得
,解得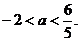
检验:若a=-2,则原不等式为 ,解集是空集,满足题意;若
,解集是空集,满足题意;若 ,则原不等式为
,则原不等式为 ,即
,即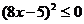 ,解得
,解得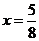 ,不满足题意。
,不满足题意。
故正确答案为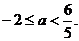
切记:解填空题应方法恰当,争取一步到位,答题形式标准,避免丢三落四,“一知半解”。
6、变法检验。一种方法解答之后,再用其它方法解之,看它们的结果是否一致,从而可避免方法单一造成的策略性错误。
例23、若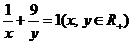 ,则
,则 的最小值是 。
的最小值是 。
错解: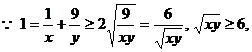
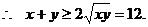
检验:上述错解在于两次使用重要不等式,等号不可能同时取到。
换一种解法为:


5、作图检验。当问题具有几何背景时,可通过作图进行检验,以避免一些脱离事实而主观臆断致错。
 例22、函数
例22、函数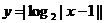 的递增区间是 。
的递增区间是 。
错解:
检验:由
作图可知正确答案为
4、估算检验。当解题过程是否等价变形难以把握时,可用估算的方法进行检验,以避免忽视充要条件而产生逻辑性错误。
例21、不等式 的解是 。
的解是 。
错解:两边平行得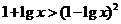 ,即
,即 ,解得
,解得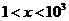 。
。
检验:先求定义域得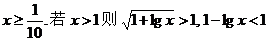 ,原不等式成立;若
,原不等式成立;若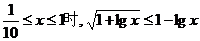 ,原不等式不成立,故正确答案为x>1。
,原不等式不成立,故正确答案为x>1。
3、逆代检验。若答案是有限的、具体的数据时,可逐一代入进行检验,以避免因扩大自变量的允许值范围而产生增解致错。
例20、方程 的解是 。
的解是 。
错解:设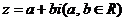 ,则
,则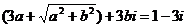 ,根据复数相等的定义得
,根据复数相等的定义得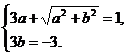 解得
解得 。故
。故
检验:若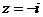 ,则原方程成立;若
,则原方程成立;若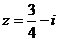 ,则原方程不成立。
,则原方程不成立。
故原方程有且只有一解z=-i.
2、赋值检验。若答案是无限的、一般性结论时,可赋予一个或几个特殊值进行检验,以避免知识性错误。
例19、已知数列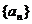 的前n项和为
的前n项和为 ,则通项公式
,则通项公式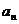 = 。
= 。
错解: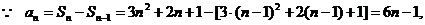
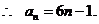
检验:取n=1时,由条件得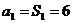 ,但由结论得a1=5。
,但由结论得a1=5。
故正确答案为
1、回顾检验
例18、满足条件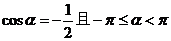 的角
的角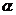 的集合为 。
的集合为 。
错解:
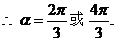
检验:根据题意,答案中的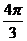 不满足条件
不满足条件 ,应改为
,应改为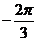 ;其次,角
;其次,角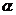 的取值要用集合表示。故正确答案为
的取值要用集合表示。故正确答案为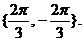
6、分析法:根据题设条件的特征进行观察、分析,从而得出正确的结论。
例16、如右图,在直四棱柱 中,当底面四边形满足条件
时,有
中,当底面四边形满足条件
时,有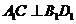 (填上你认为正确的一个条件
(填上你认为正确的一个条件
即可,不必考虑所有可能性的情形)。
解:因四棱柱 为直四棱柱,故
为直四棱柱,故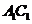 为
为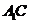 在面
在面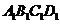 上的射影,从而要使
上的射影,从而要使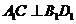 ,只要
,只要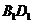 与
与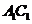 垂直,故底面四边形
垂直,故底面四边形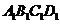 只要满足条件
只要满足条件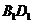

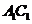 即可。
即可。
例17、以双曲线 的左焦点F,左准线l为相应的焦点和准线的椭圆截直线
的左焦点F,左准线l为相应的焦点和准线的椭圆截直线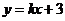 所得的弦恰好被x轴平分,则k的取值范围是
。
所得的弦恰好被x轴平分,则k的取值范围是
。
解:左焦点F为(-2,0),左准线l:x =-,因椭圆截直线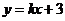 所得的弦恰好被x轴平分,故根据椭圆的对称性知,椭圆的中心即为直线
所得的弦恰好被x轴平分,故根据椭圆的对称性知,椭圆的中心即为直线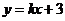 与x轴的交点
与x轴的交点 ,由
,由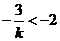 ,得0 < k < 。
,得0 < k < 。
5、构造法:根据题设条件与结论的特殊性,构造出一些新的数学形式,并借助于它认识和解决问题的一种方法。
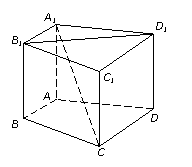
 例13、如图,点P在正方形ABCD所在的平面外,PD⊥ABCD,PD=AD,则PA与BD所成角的度数为 。
例13、如图,点P在正方形ABCD所在的平面外,PD⊥ABCD,PD=AD,则PA与BD所成角的度数为 。
解:根据题意可将此图补形成一正方体,在正方体中易求得PA与BD所成角为60°。
例14、4个不同的小球放入编号为1,2,3,4的4个盒中,则只有1个空盒的放法共有 种(用数字作答)。
解:符合条件的放法是:有一个盒中放2个球,有2个盒中各放1个球。因此可先将球分成3堆(一堆2个,其余2堆各1个,即构造了球的“堆”),然后从4个盒中选出3个盒放3堆球,依分步计算原理,符合条件的放法有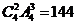 (种)。
(种)。
例15、椭圆 的焦点F1、F2,点P是椭圆上动点,当∠F1PF2为钝角时,点P的横坐标的取值范围是
 解:构造圆x2+y2=5,与椭圆 联立求得交点x02 =
解:构造圆x2+y2=5,与椭圆 联立求得交点x02 =
 x0∈(- ,)
x0∈(- ,)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com