
6. 解析: 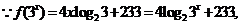



7.解:当x∈(0,+∞) 时,有-x∈(-∞,0),注意到函数f(x) 是定义在 (-∞,+∞)上的偶函数,于是,有f(x)=f(-x)=-x-(-x)4=-x-x4 .从而应填-x-x4.
5. 解:令 ,令
,令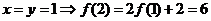 ;
;
令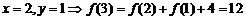 ,再令
,再令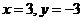 得
得
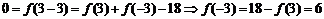
4.答案:∵ ,∴
,∴ 是定义域上的减函数,所以
是定义域上的减函数,所以 ,
, ,∴
,∴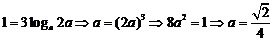
3.解:当 时,若
时,若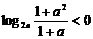 ,则
,则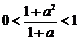
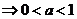 ,∴
,∴
当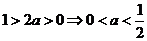 时,若
时,若 ,则
,则
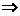
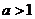 ,此时无解!
,此时无解!
所以 的取值范围是
的取值范围是
2.答案:当 时,∵函数
时,∵函数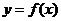 是R上的偶函数,且在
是R上的偶函数,且在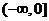 上是增函数,∴
上是增函数,∴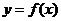 在
在 上是减函数,所以若
上是减函数,所以若 ,则
,则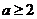 ,当
,当 时,函数
时,函数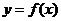 是R上的偶函数,且在
是R上的偶函数,且在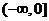 上增函数,且
上增函数,且 ,∴实数
,∴实数 的取值范围是
的取值范围是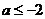
1. 答案: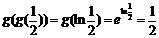 .点评:本题考察分段函数的表达式、指对数的运算.
.点评:本题考察分段函数的表达式、指对数的运算.
8.定义在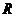 上的偶函数
上的偶函数 满足:
满足: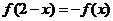 ,且在
,且在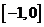 上是增函数,下面关于
上是增函数,下面关于 的判断:①
的判断:① 是周期函数;②
是周期函数;② =0;③
=0;③ 在
在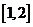 上是减函数;④
上是减函数;④ 在
在 上是减函数.其中正确的判断是 (把你认为正确的判断都填上)
上是减函数.其中正确的判断是 (把你认为正确的判断都填上)
二 感悟解答
7.已知函数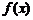 是定义在
是定义在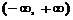 上的偶函数. 当
上的偶函数. 当 时,
时,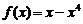 ,则 当
,则 当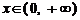 时,
时, .
.
6. (08山东卷)已知 ,则
,则 的值
的值
等于 .
考点2、函数的性质:奇偶性、单调性、周期性、函数与方程
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com