
9.电饭锅工作时有两种状态:一种是锅内水烧干前的加热状态,另一种是锅内水烧干后的保温状态.如图3-32所示是电饭锅的电路原理示意图,S是用感温材料制造的开关,下列说法中正确的是 ( )
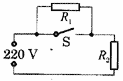
A.其中R2是供加热用的电阻丝
B.当开关S接通时电饭锅为加热状态,S断开时为保温状态
C.要使R2在保温状态时的功率为加热状态时功率的一半,R1/R2应为2∶1
D.要使R2在保温状态时的功率为加热状态时的一关,R1/R2应为( -1)∶1
-1)∶1
7.如图所示,实线表示处在竖直平面内的匀强电场的电场线,与水平方向成α角,水平方向的匀强磁场与电场正交,有一带电液滴沿斜向上的虚线L做直线运动,L与水平方向成β角,且α>β,则下列说法中正确的是( )

A.液滴一定做匀速直线运动 B.液滴一定带正电 C.电场线方向一定斜向上 D.液滴有可能做匀变速直线运动 8.如图所示,两个半径相同的半圆形轨道分别竖直放在匀强电场和匀强磁场中,轨道两端在同一高度上,轨道是光滑的.两个相同的带正电小球同时从两轨道左端最高点由静止释放,M、N为轨道的最低点,则 ( )
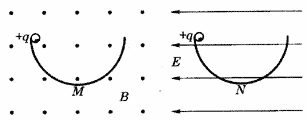
A.两小球到达轨道最低点的速度vM>vN B.两小球到达轨道最低点时对轨道的压力NM>NN C.小球第一次到达M点的时间大于小球第一次到达N点的时间 D.在磁场中小球能到达轨道的另一端,在电场中小球不能到达轨道的另一端.
5.如图所示,一个带电粒子(重力不计),从粒子源飘入(初速度很小,可忽略不计)电压为U1的加速电场,经加速后从小孔S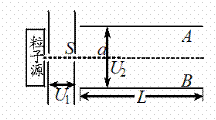 沿平行金属板A、B的中心线射入,A、B板长为L,相距为d,电压为U2。则带电粒子能从A、B板间飞出,应该满足的条件是( )
沿平行金属板A、B的中心线射入,A、B板长为L,相距为d,电压为U2。则带电粒子能从A、B板间飞出,应该满足的条件是( )
A.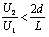
 B.
B.
C.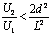 D.
D.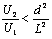
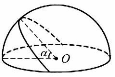
6 如图所示,电荷均匀分布在半球面上,它在这半球的中心O处电场强度等于E0.两个平面通过同一条直径,夹角为α,从半球中分出一部分球面,则所分出的这部分球面上(在 “小瓣”上)的电荷在O处的电场强度为
“小瓣”上)的电荷在O处的电场强度为 ( )
( )
 A.
A.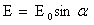 B.
B.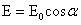
C.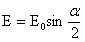 D.
D.
4.如图所示,两平行金属板水平放置,开始开关S合上使平行板电容器带电.板间存在垂直纸面向里的匀强磁场.一个不计重力的带电粒子恰能以水平向右的速度沿直线通过两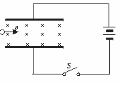 板.在以下方法中,能使带电粒子仍沿水平直线通过两板的是 ( )
板.在以下方法中,能使带电粒子仍沿水平直线通过两板的是 ( )
A.把两板的距离减小一半,同时把粒子速率增加一倍
B.把两板的距离增大一倍,同时把板间磁感应强度增大一倍
C.把开关S断开,两板的距离增大一倍,同时把板间磁场的磁感应强度减为一半
 D.把开关S断开,两板的距离减小一半,同时把粒子速率减小一半
D.把开关S断开,两板的距离减小一半,同时把粒子速率减小一半
2.下列说法正确的是( )
A.电荷放在电势高的地方,电势能就大
B.无论正电荷还是负电荷,克服电场力做功它的电势能都增大
C.正电荷在电场中某点的电势能,一定大于负电荷在该点具有的电势能
D.电场强度为零的点,电势一定为零
3 一束带电粒子以同一速度,并从同一位置进入匀强磁场,在磁场中它们的轨迹如图所示.粒子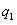 的轨迹半径为
的轨迹半径为 ,粒子
,粒子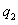 的轨迹半径为
的轨迹半径为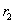 ,且
,且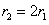 ,
,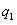 、
、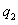 分别是它们的带
分别是它们的带 电量,则
(
)
电量,则
(
)
A.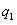 带正电、
带正电、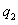 带负电,荷质比之比为
带负电,荷质比之比为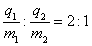
B.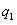 带正电、
带正电、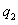 带负电,荷质比之比为
带负电,荷质比之比为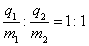
C.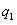 带负电、
带负电、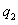 带正电,荷质比之比为
带正电,荷质比之比为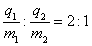
D.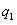 带负电、
带负电、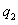 带正电,荷质比之比为
带正电,荷质比之比为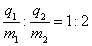
1.下列陈述中不符合历史事实的是 (  )
)
A.法拉第引入“场”的概念来研究电磁现象
B.库仑通过研究电荷间的相互作用总结出库仑定律
C.伽利略通过“理想实验”得出“力不是维持物体运动的原因”
D.开普勒发现行星运动定律并给出了万有引力定律
22.解:(1)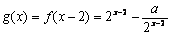 …………
…………
(2)设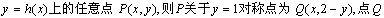
在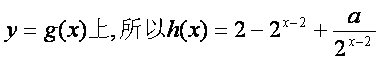 ………………………
………………………
(3)∵
∴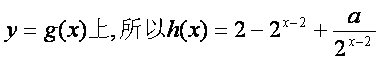
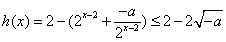
∴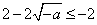
∴
21.(1)由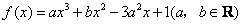 ,得
,得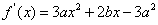

 ∴
∴
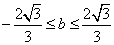
18.解;(1)(1,2)、(1、3)、(2,3)
(2)
(3)
22.(共15分)设函数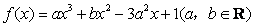 在
在 ,
,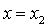 处取得极值,且
处取得极值,且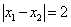 .(1)若
.(1)若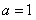 ,求
,求 的值,并求
的值,并求 的单调区间;(2)若
的单调区间;(2)若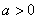 ,求
,求 的取值范围.
的取值范围.
文科数答案
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com