
20、解:(1)∵f(x)= -3·2x+5=
-3·2x+5=
…………………………1分
∴设 ,由于
,由于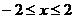 ,则
,则 …………………3分
…………………3分
∴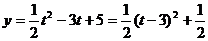 …………………………4分
…………………………4分
由二次函数知识,得:当 ,即x= -2时,y有最大值为
,即x= -2时,y有最大值为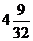 ………6分
………6分
(2)∵ =
= …………………7分
…………………7分
设 ,则
,则 …………………8分
…………………8分
①当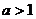 时,由于
时,由于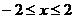 ,则
,则 …………………9
…………………9
由二次函数知识,得:当 ,即x=2时,y有最大值14
,即x=2时,y有最大值14
∴ …………………………10分
…………………………10分
解得 (舍去),
(舍去), (舍去),
(舍去), …………………11分
…………………11分
②当 时,由于
时,由于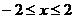 ,则
,则 ……………………12分
……………………12分
由二次函数知识,得:当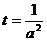 ,即x=-2时,y有最大值14
,即x=-2时,y有最大值14
∴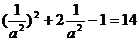 …………………………13分
…………………………13分
解得:
综上所述, ,或
,或 …………………………14分
…………………………14分
(其他解法请参照给分)
21解:(1)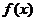 在
在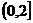 上是减函数,在
上是减函数,在 上是增函数。…………………1分
上是增函数。…………………1分
证明:设任意 ,则
,则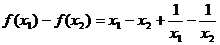 ………2分
………2分
=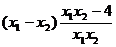 …………………3分
…………………3分
又设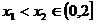 ,则
,则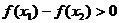 ∴
∴
∴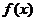 在
在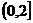 上是减函数
…………………………5分
上是减函数
…………………………5分
又设 ,则
,则 ∴
∴
∴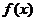 在
在 上是增函数。
…………………7分
上是增函数。
…………………7分
(2)由上及f(x)是奇函数,可猜想:f(x)在 和
和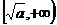 上是增函数,
上是增函数,
f(x)在 和
和 上是减函数
…………………9分
上是减函数
…………………9分
(3)∵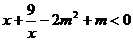 在
在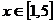 上恒成立
上恒成立
∴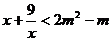 在
在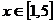 上恒成立
…………………………10分
上恒成立
…………………………10分
由(2)中结论,可知函数 在
在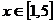 上的最大值为10,
上的最大值为10,
此时x=1 …………………………12分
要使原命题成立,当且仅当
∴ 解得
解得
∴实数m的取值范围是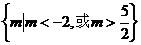 …………………………14分
…………………………14分
19、(1)解:f(x)=
……………………………3分
 画出函数f(x)的图象如右图:
画出函数f(x)的图象如右图:
除去点(0,1)和(0,-1)
…………………………6分

(2)解:f (x)为定义域上的奇函数。 ………………………… 9分
证明:
设x>0时,则-x<0
∴f(-x)= -(-x)2+1= -x2+1= -(x2-1)= -f(x) …………………………11分
设x<0时,则-x>0
∴f(-x)=(-x)2-1=x2-1= -(-x2+1)= -f(x)
∴f(x)是定义域上的奇函数 …………………………13分
18、解:(1)∵ ∴
∴ ……………………3分
……………………3分
∴ ……………………………5分
……………………………5分
∴x=2,即原方程的解为x=2 ……………………………6分
(2)∵ ∴
∴ ……………………7分
……………………7分
∴ ……………………………9分
……………………………9分
∴ ……………………………11分
……………………………11分
∴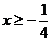 ……………………………12分
……………………………12分
∴函数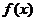 的定义域为
的定义域为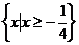 ……………………………13分
……………………………13分

17、解:(1)∵ ………4分
………4分
∴ ……………………………8分
……………………………8分
(2)∵ ……………………………10分
……………………………10分
∴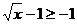 ……………………………12分
……………………………12分
∴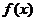 的定义域为
的定义域为 ……………………………13分
……………………………13分
解法二(换元法)设 ……………………………2分
……………………………2分
则 ……………………………4分
……………………………4分
∴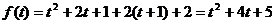 ……………………7分
……………………7分
∴ ……………………………8分
……………………………8分
(2)∵ ……………………………10分
……………………………10分
∴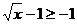 ……………………………12分
……………………………12分
∴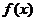 的定义域为
的定义域为 ……………………………13分
……………………………13分
16、解:(1)集合A=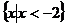 ………………………………3分
………………………………3分
∴CUA={x| }
……………………………6分
}
……………………………6分
(2)集合B=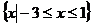 ……………………………8分
……………………………8分
∴ A∩B=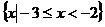 ……………………………10分
……………………………10分
∴CU(A∩B)=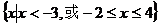 ……………………………13分
……………………………13分
11、a≤1 12、 13、4
14、
13、4
14、 15、①,⑤
15、①,⑤
21、(本小题满分14分)
(1) 判断函数f(x)= 在
在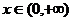 上的单调性并证明你的结论?
上的单调性并证明你的结论?
(2)猜想函数 在
在 上的单调性?(只需写出结论,不用证明)
上的单调性?(只需写出结论,不用证明)
(3)利用题(2)的结论,求使不等式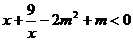 在
在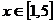 上恒成立时的实数m的取值范围?
上恒成立时的实数m的取值范围?
“华安、连城、永安、漳平一中,龙海二中,泉港一中” 四地六校联考
2010-2011学年上学期第一次月考
高一数学试卷
(考试时间:120分钟 总分:150分)
20、(本小题满分14分)
(1)求函数f(x)= -3·2x+5在区间[-2,2]上的最大值,并求函数f(x)取得最大值时的x的取值?
-3·2x+5在区间[-2,2]上的最大值,并求函数f(x)取得最大值时的x的取值?
(2)若函数 在区间
在区间 上的最大值为14,求实数a的值?
上的最大值为14,求实数a的值?
19、(本小题满分13分)
已知函数f(x)=x|x|-
1)化简f(x)的解析式,并画出f(x)的图象?
2)判断f(x)的奇偶性并证明你的结论?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com