3．(2008·山东卷)设函数f(x)＝|x+1|+|x－a|的图象关于直线x＝1对称，则a的值为(　)

A．3　 　　　　　　　　　　　　　　　　　　　 B．2

C．1　 　 　　　　　　　　　　　　　　　　　 D．－1

[解析]　∵f(x)图象关于x＝1对称，

∴f(1+x)＝f(1－x)

∴|x+1－a|＝|x－2|且|x+2|＝|x+a－1|

∴1－a＝－2，∴a＝3，故选A.

[答案]　A

2．(2009·安徽卷理)若集合

A＝{x||2x－1|＜3}，B＝，则A∩B是

(　)

A．{x|－1＜x＜－或2＜x＜3}

B．{x|2＜x＜3}

C．{x|－＜x＜2}

D．{x|－1＜x＜－}

[解析]　集合A＝{x|－1＜x＜2}，B＝{x|x＜－或x＞3}，

∴A∩B＝{x|－1＜x＜－}

[答案]　D

1．若a，b都是非零实数，则下列不等式不恒成立的是

(　)

A．|a+b|≥a－b　 　　　　　　　　　　　　　　 B．a²+b²≥2|a·b|

C．|a+b|≤|a|+|b|　 　　　　　　　　　　　　 D．|+|≥2

[答案]　A

12．(2008·佛山一模)如图A、B是单位圆O上的点，C是圆与x轴正半轴的交点，A点的坐标为(，)，三角形AOB为正三角形．

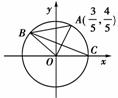
(1)求sin∠COA；

(2)求|BC|²的值．

[解]　(1)因为A点的坐标为(，)，根据三角函数定义可知y＝，r＝1

所以sin∠COA＝＝.

(2)因为三角形AOB为正三角形，所以∠AOB＝60°，sin∠COA＝，cos∠COA＝.

所以cos∠COB＝cos(∠COB+60°)＝cos∠COBcos60°－sin∠COBsin60°

＝·－·＝

所以|BC|²＝|OC|²+|OB|²－2|OC||OB|cos∠BOC

＝1+1－2×＝.

亲爱的同学请你写上学习心得

________________________________________________________________________

11．(1)设90°＜α＜180°，角α的终边上一点为P(x，)，且cosα＝x，求sinα与tanα的值；

(2)已知角θ的终边上有一点P(x，－1)(x≠0)，且tanθ＝－x，求sinθ，cosθ.

[解]　(1)∵r＝，∴cosα＝，

从而x＝，解得x＝0或x＝±.

∵90°＜α＜180°，∴x＜0，因此x＝－.

故r＝2，sinα＝＝，

tanα＝＝－.

(2)∵θ的终边过点(x，－1)(x≠0)，

∴tanθ＝－，又tanθ＝－x，

∴x²＝1，∴x＝±1.

当x＝1时，sinθ＝－，cosθ＝.

当x＝－1时，sinθ＝－，cosθ＝－.

10．若f(tanα)＝sin2α，则f(－1)的值是________．

[解析]　f(－1)＝f[tan(－)]＝－sin＝－1.

[答案]　－1

9．已知cosx＝且x是第二、第三象限角，则实数a的取值范围是________．

[解析]　∵x是第二、三象限的角

∴－1＜cosx<0即－1＜<0

解得：－＜a<.

[答案]　－＜a<

8．(2008·北京)若角α的终边经过点P(1，－2)，则tan2α的值为________．

[解析]　∵tanα＝＝－2，∴tan2α＝＝.

[答案]　

7．若－＜α＜β＜，则角α－β的取值范围是________．

[答案]　(－π，0)

6．已知一圆弧的弧长等于它所在圆的内接正三角形的边长，则这段弧所对的圆心角的弧度数为

(　)

A.　 　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　 D．2

[解析]　设圆的半径为r，则内接正三角形边长为r.∴α＝＝.

[答案]　C