
3.香蕉栽培品种多为三倍体,其繁殖方式缺少遗传变异性,且由香蕉束顶病毒引起的香蕉束顶病,对香蕉生产的危害十分严重。下列有关生产中的针对性措施不包括( )
A.可以利用此病毒抗原的特异性获得抗血清,通过抗原--抗体的凝集反应,判断 香蕉苗是否染有病毒
B.监控香蕉苗的染毒情况可利用DNA分子杂交技术,用DNA探针检测
C.采用基因工程,对香蕉的抗病毒能力进行针对性改良
D.采用杂交育种,获得新的香蕉品系提高抗病能力
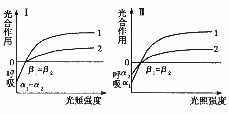
2.下面有关光合作用与细胞呼吸的曲线图示正确的是( )
1代表典型的喜阳植物
2代表典型的喜阴植物
α表示植物在黑暗中细胞呼吸放出CO2的量
β表示光补偿点(即光合作用吸收CO2的量等于细胞呼吸放出CO2的量时的光强度)

A B C D
1.下列生命活动与生物膜功能无直接关系的是( )
A.胰岛β细胞分泌胰岛素 B.氨基酸脱水缩合
C.递质在突触中传递信息 D.受精作用的完成
22. (本题满分14分)已知定点C(-1,0)及椭圆x2+3y2=5,过点C的动直线与椭圆相交于A,B两点.
(本题满分14分)已知定点C(-1,0)及椭圆x2+3y2=5,过点C的动直线与椭圆相交于A,B两点.
(1)若线段AB中点的横坐标是- ,求直线AB的方程;
,求直线AB的方程;
(2)在x轴上是否存在点M,使 为常数?若存在,求出点M的坐标;若不存在,请说明理由.
为常数?若存在,求出点M的坐标;若不存在,请说明理由.
解 (1)依题意,直线AB的斜率存在,设直线AB的方程为y=k(x+1),
将y=k(x+1)代入x2+3y2=5,
消去y整理得(3k2+1)x2+6k2x+3k2-5=0. …………2 分
设A(x1,y1),B(x2,y2),
 则
则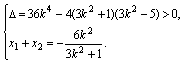 …………4分
…………4分
由线段AB中点的横坐标是- ,
,
得 =-
=- =-
=- ,解得k=±
,解得k=± ,适合①.
……………6分
,适合①.
……………6分
所以直线AB的方程为x-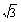 y+1=0,或x+
y+1=0,或x+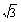 y+1=0.………………7分
y+1=0.………………7分
(2)假设在x轴上存在点M(m,0),使 为常数.
为常数.
(ⅰ)当直线AB与x轴不垂直时,由(1)知
x1+x2=- ,x1x2=
,x1x2= .
③
.
③
所以 =(x1-m)(x2-m)+y1y2
=(x1-m)(x2-m)+y1y2
=(x1-m)(x2-m)+k2(x1+1)(x2+1)
=(k2+1)x1x2+(k2-m)(x1+x2)+k2+m2. …………9分
将③代入,整理得
 =
= +m2
+m2
= +m2
+m2
=m2+2m- -
- . ………………11分
. ………………11分
注意到 是与k无关的常数,从而有
是与k无关的常数,从而有
6m+14=0,m=- ,此时
,此时 =
= . ………………12分
. ………………12分
(ⅱ)当直线AB与x轴垂直时,
此时点A,B的坐标分别为
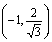 、
、 ,
,
当m=- 时,亦有
时,亦有 =
= .
.
综上,在x轴上存在定点M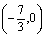 ,使
,使 为常数. …………14分
为常数. …………14分
21. (本题满分15分)已知二次函数
(本题满分15分)已知二次函数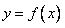 的图像经过坐标原点,其导函数f'(x)=2x+2,数列
的图像经过坐标原点,其导函数f'(x)=2x+2,数列 的前n项和为
的前n项和为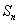 ,点(n,Sn)(n∈N*)均在函数
,点(n,Sn)(n∈N*)均在函数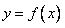 的图像上.
的图像上.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设bn= ,Tn是数列{bn}的前n项和,求
,Tn是数列{bn}的前n项和,求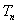 .
.
解:(1)f(x)=x2+2x ………… 2分
所以,Sn=n2+2n,当n=1,a1=S1=3,当n≥2时,an=Sn-Sn-1=2n+1,
∴an=2n+1(n∈N*) ………………6分
(2)
因为bn= ………… 10分
………… 10分
所以Tn=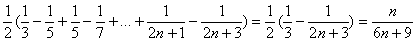 …15分
…15分
20. (本题满分15分).已知函数
(本题满分15分).已知函数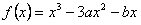 ,其中
,其中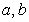 为实数.
为实数.
(Ⅰ) 若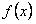 在
在 处取得的极值为
处取得的极值为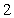 ,求
,求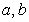 的值;
的值;
(Ⅱ)若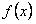 在区间
在区间 上为减函数,且
上为减函数,且 ,求
,求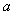 的取值范围.
的取值范围.
解 (Ⅰ)由题设可知:
 且
且 ,
………………
3分
,
………………
3分
即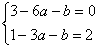 ,解得
,解得 ……………… 6分
……………… 6分
(Ⅱ) ,
………………
8分
,
………………
8分
又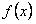 在
在 上为减函数,
上为减函数,

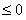 对
对 恒成立,
………………
10分
恒成立,
………………
10分
即 对
对 恒成立.
恒成立.

 且
且
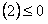 ,
………………
13分
,
………………
13分
即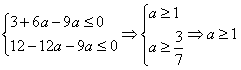 ,
,

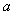 的取值范围是
的取值范围是 ……………… 15分
……………… 15分
19. (本题满分14分)已知
(本题满分14分)已知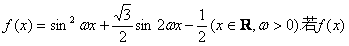 的最小正周期为
的最小正周期为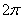 。
。
(I)求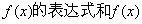 的单调递增区间;
的单调递增区间;
(II)求 的最大值和最小值
的最大值和最小值
解:(I)由已知
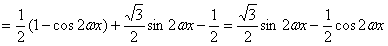
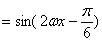 ………………3分
………………3分
又由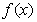 的周期为
的周期为 ,故
,故 …………4分
…………4分
 …………5分
…………5分

即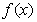 的单调递增区间为
的单调递增区间为 ……7分
……7分
(II) …………10分
…………10分

 …………14分
…………14分
18. (本题满分14分)平面内给定三个向量a=(3,2),b=(-1,2),c=(4,1).回答下列问题:
(本题满分14分)平面内给定三个向量a=(3,2),b=(-1,2),c=(4,1).回答下列问题:
(1)若(a+kc)∥(2b-a),求实数k;
(2)设d=(x,y)满足(d-c)∥(a+b)且|d-c|=1,求d.
解 (1)∵(a+kc)∥(2b-a),
又a+kc=(3+4k,2+k),2b-a=(-5,2), ……………… 2分
∴2×(3+4k)-(-5)×(2+k)=0, …… 4分 ∴k=-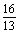 . ………… 6分
. ………… 6分
(2)∵d-c=(x-4,y-1),a+b=(2,4), 又(d-c)∥(a+b)且|d-c|=1,……8分
∴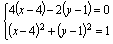 , ………… 10分
, ………… 10分
解得 或
或 .
………… 12分
.
………… 12分
∴d= 或d=
或d= . ………… 14分
. ………… 14分
11. [2,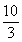 ] 12. (1,2] 13.-25 14.
] 12. (1,2] 13.-25 14. 15.2010 16.20 17.30
15.2010 16.20 17.30
非选择题部分(共100分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com