
13.已知点A(1,2),直线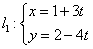 (t为参数)与直线
(t为参数)与直线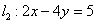 相交于点B,则A、B两点之间的距离|AB|=
相交于点B,则A、B两点之间的距离|AB|=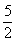 .
.
[解析]将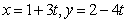 代入
代入 ,得
,得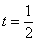 ,所以|AB|=5t=
,所以|AB|=5t=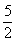 .
.
12.已知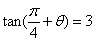 ,则
,则 的值为
的值为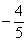 .
.
[解析]由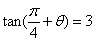 ,得
,得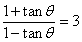 ,解得
,解得 .
.
所以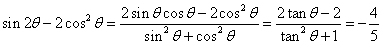 .
.
11.先后抛掷两枚质地均匀的正方体骰子,抛掷第一枚骰子得到的点数记为x,抛掷第二枚骰子得到的点数记为y,则使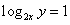 的概率为
的概率为 .
.
[解析]由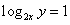 ,得
,得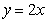 ,则
,则 或
或 或
或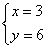 ,故
,故 .
.
10.在△ABC中,已知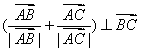 ,且
,且 ,则△ABC的形状是
,则△ABC的形状是
等边三角形 .
[解析]由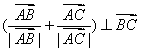 ,得∠BAC的平分线垂直于BC,所以
,得∠BAC的平分线垂直于BC,所以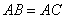 .
.
由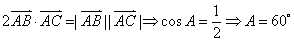 ,故△ABC为等边三角形.
,故△ABC为等边三角形.
9.不等式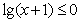 的解集是 (-1,0] .
的解集是 (-1,0] .
[解析]由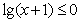 ,得
,得 .
.
8.设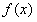 与
与 是定义在同一区间[a,b]上的两个函数,若对任意x∈[a,b],都有
是定义在同一区间[a,b]上的两个函数,若对任意x∈[a,b],都有
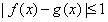 成立,则称
成立,则称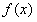 和
和 在[a,b]上是“密切函数”,区间[a,b]称为“密切区间”.若
在[a,b]上是“密切函数”,区间[a,b]称为“密切区间”.若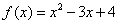 与
与 在[a,b]上是“密切函数”,则其“密切区间”可以是 ( D )
在[a,b]上是“密切函数”,则其“密切区间”可以是 ( D )
A. [1,4] B. [2,4] C. [3,4] D. [2,3]
[解析]因为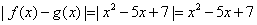 .由
.由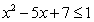 ,得
,得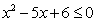 ,解得
,解得 ,故选D.
,故选D.
7.一艘海轮从A处出发,以每小时40海里的速度沿东偏南50°方向直线航行,30分钟后到达B处.在C处有一座灯塔,海轮在A处观察灯塔,其方向是东偏南20°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点间的距离是 ( A )
A. 海里
B.
海里
B. 海里
C.
海里
C.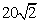 海里 D.
海里 D.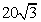 海里
海里
[ 解析]如图,由已知可得,∠BAC=30°,∠ABC=105°,
解析]如图,由已知可得,∠BAC=30°,∠ABC=105°,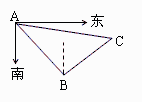
AB=20,从而∠ACB=45°.
在△ABC中,由正弦定理,得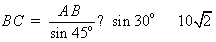 .
.
故选A.
6.给出下列四个命题:
①垂直于同一平面的两条直线相互平行;
②垂直于同一平面的两个平面相互平行;
③若一个平面内有无数条直线与另一个平面都平行,那么这两个平面相互平行;
④若一条直线垂直于一个平面内的任一直线,那么这条直线垂直于这个平面.
其中真命题的个数是
 ( B )
( B )
A.1个
B.2个
C. 3个
D.4个
3个
D.4个
[解析]命题①,④为真, 命题②,③为假,故选B.
5.某景泰蓝厂为了制作国庆六十周年的纪念品,需要一种特殊的蓝色釉料.此种釉料需要用石英、云石、硼砂等矿物质,再加某种化工原料合制而成.为了寻找最合适的配方,需要在单位用量(10,28)的试验范围内寻找该种化工原料的最佳配用量,考虑到试验的工序多时间长,现决定用均分分批试验法安排试验,每批试验安排8个试点,则第二批试验后存优范围的区间长度是( C )
A. 0.4 B.0.5 C.0.8 D. 1
[解析]将区间(10,28) 均分为9等份,在8个分点处各做一次试验,则第一批试验后存优范围的区间长度为4.
设第一批试验后的存优范围是 ,将该区间均分为10等份,在新增的8个分点处各做一次试验,则第二批试验后存优范围的区间长度为0.8,故选C.
,将该区间均分为10等份,在新增的8个分点处各做一次试验,则第二批试验后存优范围的区间长度为0.8,故选C.
4.将函数 的图象向上平移1个单位,再向右平移
的图象向上平移1个单位,再向右平移 个单位,所得图象对应的函数解析式是
( A )
个单位,所得图象对应的函数解析式是
( A )
A.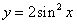 B.
B. C.
C.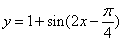 D.
D.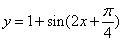
[解析]将函数 的图象向上
的图象向上 平移1个单位,得到函数
平移1个单位,得到函数 的图象,再向右平移
的图象,再向右平移 个单位,得到函数
个单位,得到函数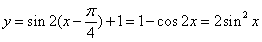 的图象,故选A.
的图象,故选A.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com