例1．一个人带三只狼和三只羚羊过河，只有一条船，同船可以容纳一个人和两只动物。没有人在的时候，如果狼的数量不少于羚羊的数量，狼就会吃掉羚羊。(1)设计过河的算法；(2)思考每一步算法所遵循的相同之处原则是什么。

解：算法或步骤如下：

S1　 人带两只狼过河

S2　 人自己返回

S3　 人带一只羚羊过河

S4　 人带两只狼返回

S5　 人带两只羚羊过河

S6　 人自己返回

S7　 人带两只狼过河

S8　 人自己返回带一只狼过河

例2．写出一个求有限整数序列中的最大值的算法。

解：为了便于理解，算法步骤用自然语言叙述：

　 先将序列中的第一个整数设为最大值；

　 将序列中的下一个整数值与“最大值”比较，如果它大于此“最大值”，这时就假定“最大值”就是这个整数；

　 如果序列中还有其它整数，重复 ；

　 在序列中一直进行到没有可比的数为止，这时假定的“最大值”就是这个序列中的最大值。

试用数学语言写出对任意3个整数 中最大值的求法

　 max=a

　 如果b>max，则max=b

　 如果c>max，则max=c,

　 max就是 中的最大值。

　　 算法的概念：由基本运算及规定的运算顺序所构成的完整的解题步骤，或者是按照要求设计好的有限的计算序列，并且这样的步骤或序列能解决一类问题。

算法的五个重要特征：

(1)有穷性：一个算法必须保证执行有限步后结束；

(2)确切性：算法的每一步必须有确切的定义；

(3)可行性：算法原则上能够精确地运行，而且人们用笔和纸做有限次即可完成；

(4)输入：一个算法有0个或多个输入，以刻划运算对象的初始条件。所谓0个输入是指算法本身定出了初始条件。

(5)输出：一个算法有1个或多个输出，以反映对输入数据加工后的结果。没有输出的算法是毫无意义的。

2．一群小兔一群鸡，两群合到一群里，要数腿共48，要数脑袋整17，多少小兔多少鸡？

先列方程组解题，得鸡10只，兔7只；

再归纳一般二元一次方程组的通用方法，即用高斯消去法解一般的二元一次方程组 。

令D ，若D ，方程组无解或有无数多解。

若D ，则 ， 。

由此可得解二元一次方程组的算法。

　 计算 ；

　 如果 ，则原方程组无解或有无穷多组解；否则( )，

，

　 输出计算结果 、 或者无法求解的信息。

请大家研究解决下面的一个问题

1．两个大人和两个小孩一起渡河，渡口只有一条小船，每次只能渡1 个大人或两个小孩，他们四人都会划船，但都不会游泳。试问他们怎样渡过河去？请写出一个渡河方案。

(通过学生讨论得出渡河方案与步骤如下)

S₁　 两个小孩同船过河去；

S₂　 一个小孩划船回来；

S₃　 一个大人划船过河去；

S₄ 　对岸的小孩划船回来；

S₅　 两个小孩同船渡过河去；

S₆　 一个小孩划船回来；

S₇　 余下的一个大人独自划船渡过河去；对岸的小孩划船回来；

S₈　 两个小孩再同时划船渡过河去。

　 解析：关键是理解问题发现规律

3．求次多项式当(是任意实数)的值

解析：把次多项式改写如下形式：

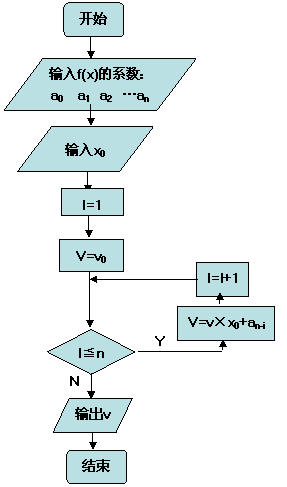
　 发现规律结合所掌握算法，通过模仿，操作，探索，寻找解决问题的通法。]

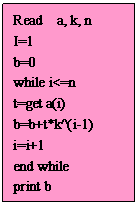　 1．用程序把进制数(共有位)转换为十进制数

2．把一个十进制数化为k进制数 　

Begin

Read　 a , k

i=1

Do

　 r=mod(a,k)

　 a(i)=r

　 a=(a-r)/k

　 i=i+1

Loop Until a=0

m=i-1

For j=m to 1 Step -1

Print a(j);

Next j

Prin “(”;k;”)”

End

设_n是邮车从第n个(1≤n＜m，n∈N^* )城市出发时邮车上邮袋的个数，设计一个算法，对任给两个正数m＞n，求_n.

分析:到达第n个城市时,邮袋个数为前一个城市的邮袋个数减去前面城市发往该市的n-1个邮袋，再加上发往后面各城市的(m-n)个邮袋，可用循环计算I从1至n时，_n的变化。

解：　伪代码为：

Read m,n

If　 m≤n then Print“错误！m必须大于n”

Else

　　 S←0

For I　 from 1 to n

　　 S←S+(m- I)-(I-1)

Next I

End For

End If

Print S

For n from 100 to 999

←int(n/100)

←int((n-100x)/10)

z←n－100－10

If n=³+³+z³ then

Pint n

End If

Next n

End for

S=0

For I from 1 to 3

S←(S+1)/2

End For

Pint S