22.(本小题满分14分)

已知函数y=ax²+bx+c(a≠0)图象上有两点A₁(m₁,y₁),A₂(m₂,y₂),满足a²+(y₁+y₂)a+y₁·y₂=0,

求证：

(1)存在i∈{1,2},使y_i=－a;

(2)抛物线y=ax²+bx+c与x轴总有两个不同的交点；

(3)若使该图象与x轴交点为(x₁,0)(x₂,0),(x₁＜x₂＝,则存在i∈{1,2}，使x₁＜m_i＜x₂.

21.(本小题满分12分)

已知曲线C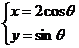： (θ为参数)，若A、B是曲线C上关于坐标轴不对称的任意两点.

(1)求AB的垂直平分线l在x轴上截距的取值范围；

(2)设过点M(1，0)的直线l是曲线C上A，B两点连线的垂直平分线，求l的斜率k的取值范围.

20.(本小题满分12分)

已知向量a=(－2，sinθ),b=(cosθ,1),其中θ∈(－,).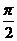

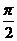(1)若a⊥b,求θ的值；

(2)令c=a－b,求|c|的最大值.

19.(本小题满分12分)

已知PA⊥平面ABCD，ABCD为矩形，M，N分别是AB，PC的中点.

(1)求证MN⊥AB；

(2)若平面PDC与平面ABCD所成的二面角为θ,能否确定θ，使直线MN是异面直线AB与PC的公垂线，若可以确定，试求θ的值，若不可以，请说明理由.

18.(本小题满分12分)

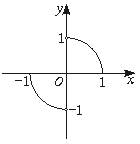
如图，函数f(x)的图象为单位圆上的两段弧，求不等式f(x)－f(－x)＞x的解集.

17.(本小题满分12分)

甲、乙、丙三位同学独立完成6道数学自测题，他们答及格的概率依次为，，.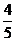

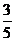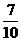求(1)三人中有且只有2人答及格的概率；

(2)三人中至少有一人不及格的概率.

16.某校要从甲、乙两名优秀短跑选手中选一名选手参加全市中学生田径百米比赛，该校预先对这两名选手测试了8次，测试成绩如下：

根据测试成绩，派_________(填甲或乙)选手参赛更好，理由是____________________.

15.设定义在R上的偶函数f(x)满足f(x+1)+f(x)=1,且当x∈［1,2］时，f(x)=2－x,则f(8.5)=_________.

14.一个长方体共一顶点的三个面的面积分别是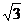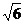，，，这个长方体对角线的长是_________.

13.抛物线y²=2x上到直线x－y+3=0距离最短的点的坐标为_________.