1、 描述向量的两个指标：模和方向.

(四)理解和巩固：

　　 例1 书本86页例1.

例2判断：

(1)平行向量是否一定方向相同？(不一定)

(2)不相等的向量是否一定不平行？(不一定)

(3)与零向量相等的向量必定是什么向量？(零向量)

(4)与任意向量都平行的向量是什么向量？(零向量)

(5)若两个向量在同一直线上，则这两个向量一定是什么向量？(平行向量)

(6)两个非零向量相等的当且仅当什么？(长度相等且方向相同)

(7)共线向量一定在同一直线上吗？(不一定)

例3下列命题正确的是(　　 )　

A.a与b共线，b与c共线，则a与c也共线　

B.任意两个相等的非零向量的始点与终点是一平行四边形的四顶点　

C.向量a与b不共线，则a与b都是非零向量　

D.有相同起点的两个非零向量不平行

解：由于零向量与任一向量都共线，所以A不正确；由于数学中研究的向量是自由向量，所以两个相等的非零向量可以在同一直线上，而此时就构不成四边形，根本不可能是一个平行四边形的四个顶点，所以B不正确；向量的平行只要方向相同或相反即可，与起点是否相同无关，所以D不正确；对于C，其条件以否定形式给出，所以可从其逆否命题来入手考虑，假若a与b不都是非零向量，即a与b至少有一个是零向量，而由零向量与任一向量都共线，可有a与b共线，不符合已知条件，所以有a与b都是非零向量，所以应选C.

例4　 如图，设O是正六边形ABCDEF的中心，分别写出图中与向量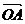、、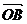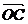相等的向量.

变式一：与向量长度相等的向量有多少个？(11个)

变式二：是否存在与向量长度相等、方向相反的向量？(存在)

变式三：与向量共线的向量有哪些？()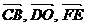

课堂练习：

1．判断下列命题是否正确，若不正确，请简述理由.　

①向量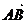与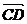是共线向量，则A、B、C、D四点必在一直线上；　

②单位向量都相等；　

③任一向量与它的相反向量不相等；　

④四边形ABCD是平行四边形当且仅当＝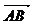

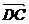
⑤一个向量方向不确定当且仅当模为0；　

⑥共线的向量，若起点不同，则终点一定不同.

解：①不正确.共线向量即平行向量，只要求方向相同或相反即可，并不要求两个向量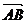、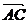在同一直线上.

②不正确.单位向量模均相等且为1，但方向并不确定.

③不正确.零向量的相反向量仍是零向量，但零向量与零向量是相等的. 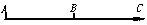④、⑤正确.⑥不正确.如图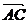与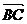共线，虽起点不同，但其终点却相同.

2．书本88页练习

(三)探究学习

1、数量与向量的区别：

数量只有大小，是一个代数量，可以进行代数运算、比较大小；

向量有方向，大小，双重性，不能比较大小.

2.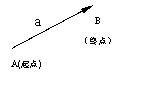向量的表示方法：

①用有向线段表示；

②用字母a、b

(黑体，印刷用)等表示；

③用有向线段的起点与终点字母：；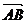

④向量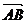的大小――长度称为向量的模，记作||.

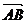3.有向线段：具有方向的线段就叫做有向线段，三个要素：起点、方向、长度.

向量与有向线段的区别：

(1)向量只有大小和方向两个要素，与起点无关，只要大小和方向相同，则这两个向量就是相同的向量；

(2)有向线段有起点、大小和方向三个要素，起点不同，尽管大小和方向相同，也是不同的有向线段.

4、零向量、单位向量概念：

①长度为0的向量叫零向量，记作0. 0的方向是任意的.

注意0与0的含义与书写区别.

②长度为1个单位长度的向量，叫单位向量.

说明：零向量、单位向量的定义都只是限制了大小.

5、平行向量定义：

①方向相同或相反的非零向量叫平行向量；②我们规定0与任一向量平行.

说明：(1)综合①、②才是平行向量的完整定义；(2)向量a、b、c平行，记作a∥b∥c.

6、相等向量定义：

长度相等且方向相同的向量叫相等向量.

说明：(1)向量a与b相等，记作a＝b；(2)零向量与零向量相等；

(3)任意两个相等的非零向量，都可用同一条有向线段来表示，并且与有向线段的起点无关.

7、共线向量与平行向量关系：

平行向量就是共线向量，这是因为任一组平行向量都可移到同一直线上(与有向线段的起点无关).

说明：(1)平行向量可以在同一直线上，要区别于两平行线的位置关系；(2)共线向量可以相互平行，要区别于在同一直线上的线段的位置关系.

(一)向量的概念：我们把既有大小又有方向的量叫向量

如图，老鼠由A向西北逃窜，猫在B处向东追去，设问：猫能否追到老鼠？(画图)

结论：猫的速度再快也没用，因为方向错了.

分析：老鼠逃窜的路线AC、猫追逐的路线BD实际上都是有方向、有长短的量.

引言：请同学指出哪些量既有大小又有方向？哪些量只有大小没有方向？

25、某中学课外兴趣小组在研究当代世界历史局势时，搜集了下列历史图片。请你为他们拟定一个最恰当的探究主题(　　 )

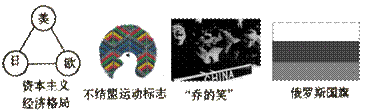
A、美国霸权地位的衰落　　　　 B、世界经济全球化

C、世界格局多极化趋势　　　　 D、第三世界的崛起

第Ⅱ卷(非选择题，共50分)