3．　 求作差向量：已知向量a、b，求作向量

　 ∵(a-b) + b = a + (-b) + b = a + 0 = a

　　　　 作法：在平面内取一点O，

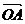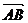　　　　　　　 作= a，　 = b

　　　　　　　 则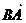= a - b

　　　　　　　 即a - b可以表示为从向量b的终点指向向量a的终点的向量.

　　　 　注意：1°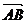表示a - b.强调：差向量“箭头”指向被减数

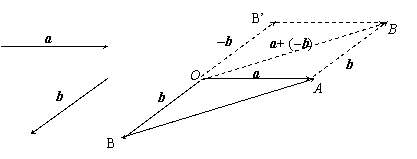　　　　　　　 2°用“相反向量”定义法作差向量，a - b = a + (-b)

　　　　　 　　　显然，此法作图较繁，但最后作图可统一.

2．　 用加法的逆运算定义向量的减法：

　 向量的减法是向量加法的逆运算：

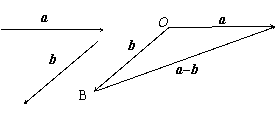　 若b + x = a，则x叫做a与b的差，记作a - b

1．　 用“相反向量”定义向量的减法

(1) “相反向量”的定义：与a长度相同、方向相反的向量.记作 -a

(2) 规定：零向量的相反向量仍是零向量.-(-a) = a.

　　 任一向量与它的相反向量的和是零向量.a + (-a) = 0

　　 如果a、b互为相反向量，则a = -b，　 b = -a，　 a + b = 0

　 (3) 向量减法的定义：向量a加上的b相反向量，叫做a与b的差.

　　 即：a - b = a + (-b)　 求两个向量差的运算叫做向量的减法.

　　　 向量加法的运算定律：

例：在四边形中，　 .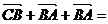

解：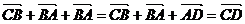

3.　　 通过阐述向量的减法运算可以转化成向量的加法运算，使学生理解事物之间可以相互转化的辩证思想.

教学重点：向量减法的概念和向量减法的作图法.

教学难点：减法运算时方向的确定.

学　 法：减法运算是加法运算的逆运算，学生在理解相反向量的基础上结合向量的加法运算掌握向量的减法运算；并利用三角形做出减向量.

教　 具：多媒体或实物投影仪，尺规

授课类型：新授课

教学思路：

2.　　 掌握向量的减法，会作两个向量的减向量，并理解其几何意义；

1.　　 了解相反向量的概念；

6、用向量加法证明：两条对角线互相平分的四边形是平行四边形

(吴春霞)

第3课时

§2.2.2　 向量的减法运算及其几何意义

教学目标：

5、已知两个力F₁，F₂的夹角是直角，且已知它们的合力F与F₁的夹角是60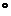，|F|=10N求F₁和F₂的大小.

4、一艘船以5km/h的速度在行驶，同时河水的流速为2km/h，则船的实际航行速度大小最大是km/h，最小是km/h