
2.运算定律
结合律:λ(μ )=(λμ)
)=(λμ) ;分配律:(λ+μ)
;分配律:(λ+μ) =λ
=λ +μ
+μ , λ(
, λ( +
+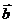 )=λ
)=λ +λ
+λ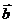
1.实数与向量的积:实数λ与向量 的积是一个向量,记作:λ
的积是一个向量,记作:λ
(1)|λ |=|λ||
|=|λ|| |;(2)λ>0时λ
|;(2)λ>0时λ 与
与 方向相同;λ<0时λ
方向相同;λ<0时λ 与
与 方向相反;λ=0时λ
方向相反;λ=0时λ =
=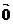
2.3平面向量的基本定理及坐标表示
第4课时
§2.3.1 平面向量基本定理
教学目的:
(1)了解平面向量基本定理;
(2)理解平面里的任何一个向量都可以用两个不共线的向量来表示,初步掌握应用向量解决实际问题的重要思想方法;
(3)能够在具体问题中适当地选取基底,使其他向量都能够用基底来表达.
教学重点:平面向量基本定理.
教学难点:平面向量基本定理的理解与应用.
授课类型:新授课
教 具:多媒体、实物投影仪
教学过程:
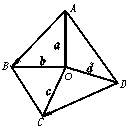
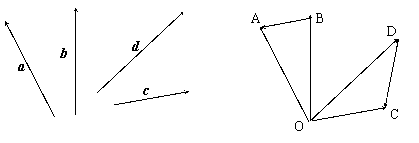
4、如图所示,O是四边形ABCD内任一点,试根据图中给出的向量,确定a、b、c、d的方向(用箭头表示),使a+b=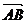 ,c-d=
,c-d=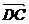 ,并画出b-c和a+d.
,并画出b-c和a+d.

(吴春霞)
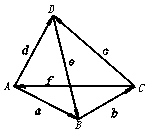
3.如图,在四边形ABCD中,根据图示填空:
a+b= ,b+c= ,c-d= ,a+b+c-d= .
2.O为平行四边形ABCD平面上的点,设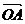 =a,
=a, 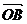 =b,
=b, 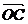 =c,
=c, 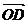 =d,则
=d,则
A.a+b+c+d=0 B.a-b+c-d=0 C.a+b-c-d=0 D.a-b-c+d=0
1.在△ABC中, 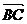 =a,
=a, 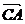 =b,则
=b,则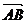 等于( )
等于( )
A.a+b? B.-a+(-b) C.a-b? D.b-a
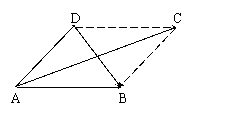
用a、b表示向量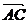 、
、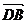 .
.
解:由平行四边形法则得:
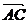 = a + b,
= a + b, 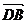 =
= 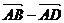 = a-b
= a-b
变式一:当a, b满足什么条件时,a+b与a-b垂直?(|a| = |b|)
变式二:当a, b满足什么条件时,|a+b| = |a-b|?(a, b互相垂直)
 变式三:a+b与a-b可能是相当向量吗?(不可能,∵ 对角线方向不同)
变式三:a+b与a-b可能是相当向量吗?(不可能,∵ 对角线方向不同)
练习:P98
解:在平面上取一点O,作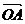 = a,
= a, 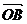 = b,
= b, 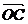 = c,
= c, 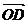 = d,
= d,
 作
作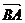 ,
, 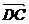 , 则
, 则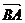 = a-b,
= a-b, 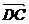 = c-d
= c-d
4. 探究:
1)如果从向量a的终点指向向量b的终点作向量,那么所得向量是b - a.
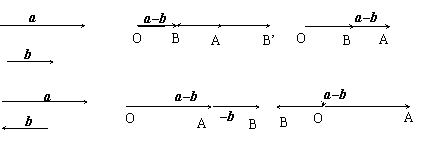
2)若a∥b, 如何作出a - b ?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com