
2.已知|a|=2,|b|=1,a与b之间的夹角为 ,那么向量m=a-4b的模为( )
,那么向量m=a-4b的模为( )
A.2
B.2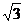 C.6
D.12
C.6
D.12
1.已知|a|=1,|b|=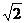 ,且(a-b)与a垂直,则a与b的夹角是( )
,且(a-b)与a垂直,则a与b的夹角是( )
A.60° B.30° C.135° D.45°
例1 已知|a|=5, |b|=4, a与b的夹角θ=120o,求a·b.
例2 已知|a|=6, |b|=4, a与b的夹角为60o求(a+2b)·(a-3b).
例3 已知|a|=3, |b|=4, 且a与b不共线,k为何值时,向量a+kb与a-kb互相垂直.
例4 判断正误,并简要说明理由.
①a·0=0;②0·a=0;③0-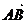 =
=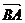 ;④|a·b|=|a||b|;⑤若a≠0,则对任一非零b有a·b≠0;⑥a·b=0,则a与b中至少有一个为0;⑦对任意向量a,b,с都有(a·b)с=a(b·с);⑧a与b是两个单位向量,则a2=b2.
;④|a·b|=|a||b|;⑤若a≠0,则对任一非零b有a·b≠0;⑥a·b=0,则a与b中至少有一个为0;⑦对任意向量a,b,с都有(a·b)с=a(b·с);⑧a与b是两个单位向量,则a2=b2.
解:上述8个命题中只有③⑧正确;
对于①:两个向量的数量积是一个实数,应有0·a=0;对于②:应有0·a=0;
对于④:由数量积定义有|a·b|=|a|·|b|·|cosθ|≤|a||b|,这里θ是a与b的夹角,只有θ=0或θ=π时,才有|a·b|=|a|·|b|;
对于⑤:若非零向量a、b垂直,有a·b=0;
对于⑥:由a·b=0可知a⊥b可以都非零;
对于⑦:若a与с共线,记a=λс.
则a·b=(λс)·b=λ(с·b)=λ(b·с),
∴(a·b)·с=λ(b·с)с=(b·с)λс=(b·с)a
若a与с不共线,则(a·b)с≠(b·с)a.
评述:这一类型题,要求学生确实把握好数量积的定义、性质、运算律.
例6 已知|a|=3,|b|=6,当①a∥b,②a⊥b,③a与b的夹角是60°时,分别求a·b.
解:①当a∥b时,若a与b同向,则它们的夹角θ=0°,
∴a·b=|a|·|b|cos0°=3×6×1=18;
若a与b反向,则它们的夹角θ=180°,
∴a·b=|a||b|cos180°=3×6×(-1)=-18;
②当a⊥b时,它们的夹角θ=90°,
∴a·b=0;
③当a与b的夹角是60°时,有
a·b=|a||b|cos60°=3×6×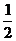 =9
=9
评述:两个向量的数量积与它们的夹角有关,其范围是[0°,180°],因此,当a∥b时,有0°或180°两种可能.
5.两个向量的数量积的性质:
设a、b为两个非零向量,e是与b同向的单位向量.
1° e×a = a×e =|a|cosq
2° a^b Û a×b = 0
3° 当a与b同向时,a×b = |a||b|;当a与b反向时,a×b = -|a||b|.
特别的a×a = |a|2或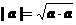
4° cosq =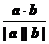
5° |a×b| ≤ |a||b|
4.向量的数量积的几何意义:
数量积a×b等于a的长度与b在a方向上投影|b|cosq的乘积.
3.“投影”的概念:作图
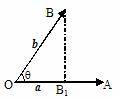
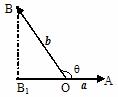
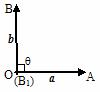
定义:|b|cosq叫做向量b在a方向上的投影.
投影也是一个数量,不是向量;当q为锐角时投影为正值;当q为钝角时投影为负值;当q为直角时投影为0;当q = 0°时投影为 |b|;当q = 180°时投影为 -|b|.
2.平面向量数量积(内积)的定义:已知两个非零向量a与b,它们的夹角是θ,则数量|a||b|cosq叫a与b的数量积,记作a×b,即有a×b = |a||b|cosq,
(0≤θ≤π).并规定0与任何向量的数量积为0.
×探究:两个向量的数量积与向量同实数积有很大区别
(1)两个向量的数量积是一个实数,不是向量,符号由cosq的符号所决定.
(2)两个向量的数量积称为内积,写成a×b;今后要学到两个向量的外积a×b,而a×b是两个向量的数量的积,书写时要严格区分.符号“· ”在向量运算中不是乘号,既不能省略,也不能用“×”代替.
(3)在实数中,若a¹0,且a×b=0,则b=0;但是在数量积中,若a¹0,且a×b=0,不能推出b=0.因为其中cosq有可能为0.
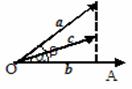 (4)已知实数a、b、c(b¹0),则ab=bc Þ a=c.但是a×b = b×c
(4)已知实数a、b、c(b¹0),则ab=bc Þ a=c.但是a×b = b×c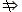 a = c
a = c
如右图:a×b = |a||b|cosb = |b||OA|,b×c = |b||c|cosa = |b||OA|
Þ a×b = b×c 但a ¹ c
(5)在实数中,有(a×b)c = a(b×c),但是(a×b)c ¹ a(b×c)
显然,这是因为左端是与c共线的向量,而右端是与a共线的向量,而一般a与c不共线.
1.两个非零向量夹角的概念
已知非零向量a与b,作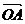 =a,
=a,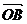 =b,则∠AOB=θ(0≤θ≤π)叫a与b的夹角.
=b,则∠AOB=θ(0≤θ≤π)叫a与b的夹角.
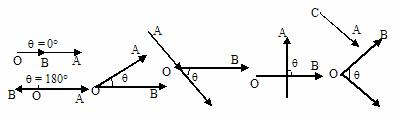
说明:(1)当θ=0时,a与b同向;
(2)当θ=π时,a与b反向;
(3)当θ=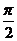 时,a与b垂直,记a⊥b;
时,a与b垂直,记a⊥b;
(4)注意在两向量的夹角定义,两向量必须是同起点的.范围0°≤q≤180°
|
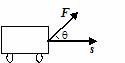
10.力做的功:W = |F|×|s|cosq,q是F与s的夹角.
9.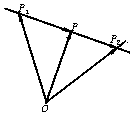 线段定比分点坐标公式的向量形式:
线段定比分点坐标公式的向量形式:
 在平面内任取一点O,设
在平面内任取一点O,设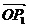 =a,
=a,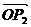 =b,
=b,
可得 =
=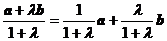 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com