
1.下列叙述不正确的是( )
A.向量的数量积满足交换律 B.向量的数量积满足分配律
C.向量的数量积满足结合律 D.a·b是一个实数
例1 已知a、b都是非零向量,且a + 3b与7a - 5b垂直,a - 4b与7a - 2b垂直,求a与b的夹角.
解:由(a + 3b)(7a - 5b) = 0 Þ 7a2 + 16a×b -15b2 = 0 ①
(a - 4b)(7a - 2b) = 0 Þ 7a2 - 30a×b + 8b2 = 0 ②
两式相减:2a×b = b2
代入①或②得:a2 = b2
设a、b的夹角为q,则cosq =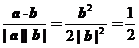 ∴q = 60°
∴q = 60°
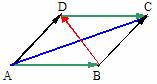
例2 求证:平行四边形两条对角线平方和等于四条边的平方和.
解:如图:平行四边形ABCD中,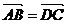 ,
,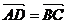 ,
,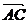 =
=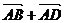
 ∴|
∴|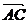 |2=
|2=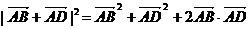
而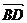 =
=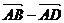 ,
,
∴|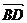 |2=
|2=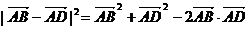
∴|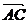 |2 + |
|2 + |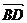 |2 = 2
|2 = 2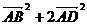 =
= 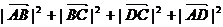
例3 四边形ABCD中,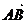 =a,
=a,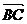 =b,
=b,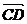 =с,
=с,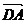 =d,且a·b=b·с=с·d=d·a,试问四边形ABCD是什么图形?
=d,且a·b=b·с=с·d=d·a,试问四边形ABCD是什么图形?
分析:四边形的形状由边角关系确定,关键是由题设条件演变、推算该四边形的边角量.
解:四边形ABCD是矩形,这是因为:
一方面:∵a+b+с+d=0,∴a+b=-(с+d),∴(a+b)2=(с+d)2
即|a|2+2a·b+|b|2=|с|2+2с·d+|d|2
由于a·b=с·d,∴|a|2+|b|2=|с|2+|d|2①
同理有|a|2+|d|2=|с|2+|b|2②
由①②可得|a|=|с|,且|b|=|d|即四边形ABCD两组对边分别相等.
∴四边形ABCD是平行四边形
另一方面,由a·b=b·с,有b(a-с)=0,而由平行四边形ABCD可得a=-с,代入上式得b·(2a)=0,即a·b=0,∴a⊥b也即AB⊥BC.
综上所述,四边形ABCD是矩形.
评述:(1)在四边形中,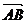 ,
,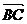 ,
,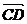 ,
,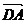 是顺次首尾相接向量,则其和向量是零向量,即a+b+с+d=0,应注意这一隐含条件应用;
是顺次首尾相接向量,则其和向量是零向量,即a+b+с+d=0,应注意这一隐含条件应用;
(2)由已知条件产生数量积的关键是构造数量积,因为数量积的定义式中含有边、角两种关系.
3.分配律:(a + b)×c = a×c + b×c
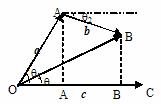
在平面内取一点O,作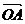 = a,
= a, 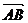 = b,
= b,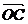 = c, ∵a + b (即
= c, ∵a + b (即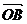 )在c方向上的投影等于a、b在c方向上的投影和,即 |a + b| cosq = |a| cosq1 + |b|
cosq2
)在c方向上的投影等于a、b在c方向上的投影和,即 |a + b| cosq = |a| cosq1 + |b|
cosq2
∴| c | |a + b| cosq =|c| |a| cosq1 + |c| |b| cosq2, ∴c×(a + b) = c×a + c×b 即:(a + b)×c = a×c + b×c
说明:(1)一般地,(a·b)с≠a(b·с)
 (2)a·с=b·с,с≠0
(2)a·с=b·с,с≠0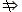 a=b
a=b
(3)有如下常用性质:a2=|a|2,
(a+b)(с+d)=a·с+a·d+b·с+b·d
(a+b)2=a2+2a·b+b2
2.数乘结合律:( a)×b =
a)×b = (a×b) = a×(
(a×b) = a×( b)
b)
证:若 > 0,(
> 0,( a)×b =
a)×b = |a||b|cosq,
|a||b|cosq,  (a×b) =
(a×b) = |a||b|cosq,a×(
|a||b|cosq,a×( b) =
b) = |a||b|cosq,
|a||b|cosq,
若 < 0,(
< 0,( a)×b =|
a)×b =| a||b|cos(p-q) = -
a||b|cos(p-q) = - |a||b|(-cosq) =
|a||b|(-cosq) = |a||b|cosq,
|a||b|cosq, (a×b) =
(a×b) = |a||b|cosq,
|a||b|cosq,
a×( b) =|a||
b) =|a|| b|cos(p-q) = -
b|cos(p-q) = - |a||b|(-cosq) =
|a||b|(-cosq) = |a||b|cosq.
|a||b|cosq.
平面向量数量积的运算律
1.交换律:a × b = b × a
证:设a,b夹角为q,则a × b = |a||b|cosq,b × a = |b||a|cosq
∴a × b = b × a
5.两个向量的数量积的性质:
设a、b为两个非零向量,e是与b同向的单位向量.
1° e×a = a×e =|a|cosq; 2° a^b Û a×b = 0
3° 当a与b同向时,a×b = |a||b|;当a与b反向时,a×b = -|a||b|.
特别的a×a = |a|2或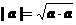
4°cosq =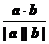 ;5°|a×b| ≤ |a||b|
;5°|a×b| ≤ |a||b|
3.“投影”的概念:作图
|
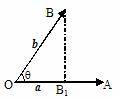
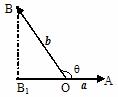
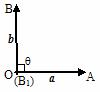
定义:|b|cosq叫做向量b在a方向上的投影.
投影也是一个数量,不是向量;当q为锐角时投影为正值;当q为钝角时投影为负值;当q为直角时投影为0;当q = 0°时投影为 |b|;当q = 180°时投影为 -|b|.
2.平面向量数量积(内积)的定义:已知两个非零向量a与b,它们的夹角是θ,则数量|a||b|cosq叫a与b的数量积,记作a×b,即有a×b = |a||b|cosq,
(0≤θ≤π).并规定0与任何向量的数量积为0.
1.两个非零向量夹角的概念
已知非零向量a与b,作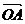 =a,
=a,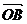 =b,则∠AOB=θ(0≤θ≤π)叫a与b的夹角.
=b,则∠AOB=θ(0≤θ≤π)叫a与b的夹角.
3.掌握两个向量共线、垂直的几何判断,会证明两向量垂直,以及能解决一些简单问题.
教学重点:平面向量数量积及运算规律.
教学难点:平面向量数量积的应用
授课类型:新授课
教 具:多媒体、实物投影仪
内容分析: 启发学生在理解数量积的运算特点的基础上,逐步把握数量积的运算律,引导学生注意数量积性质的相关问题的特点,以熟练地应用数量积的性质.
教学过程:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com