7. 向量的坐标运算(加.减.实数和向量的乘法.数量积)

6. 向量的坐标概念和坐标表示法

5. 了解实数与向量的乘法(即数乘的意义)：

4. 了解向量形式的三角形不等式：|||-||≤|±|≤||+||(试问：取等号的条件是什么?)和向量形式的平行四边形定理：2(||+||)=|－|+|+|.

3. 向量的加法的平行四边形法则(共起点)和三角形法则(首尾相接)。

2. 了解平面向量基本定理.

1. 理解向量.零向量.向量的模.单位向量.平行向量.反向量.相等向量.两向量的夹角等概念。

(王海)

第12课时

复习课

6.已知A(1，0)，B(3，1)，C(2，0)，且a=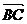，b=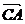，则a与b的夹角为　　　 .

5.已知A(3，2)，B(-1，-1)，若点P(x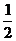，-)在线段AB的中垂线上，则x=　　 .