1．知识与技能

①通过实际问题了解指数函数的实际背景；

②理解指数函数的概念和意义，根据图象理解和掌握指数函数的性质.

③体会具体到一般数学讨论方式及数形结合的思想；

2．含有根式的式子化简，一般要先把根式转化为分数指数幂后再计算.

作业：P₆₅　　 习题2.1

A组　　 第4题

B组　 　第2题

1．　 熟练掌握有理指数幂的运算法则，化简的基础.

2．例题讲解

例1．(P₆₀，例4)计算下列各式(式中字母都是正数)

(1)

(2)

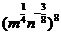
(先由学生观察以上两个式子的特征，然后分析、提问、解答)

分析：四则运算的顺序是先算乘方，再算乘除，最后算加减，有括号的先算括号的. 整数幂的运算性质及运算规律扩充到分数指数幂后，其运算顺序仍符合我们以前的四则运算顺序.

我们看到(1)小题是单项式的乘除运算；(2)小题是乘方形式的运算，它们应让如何计算呢？

其实，第(1)小题是单项式的乘除法，可以用单项式的运算顺序进行.

第(2)小题是乘方运算，可先按积的乘方计算，再按幂的乘方进行计算.

解：(1)原式=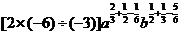

　　　　　　 =

　　　　　　 =4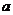

　　 (2)原式=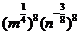

　　　　　　 =

例2．(P₆₁ 例5)计算下列各式

(1)

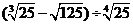
(2)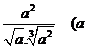＞0)

分析：在第(1)小题中，只含有根式，且不是同类根式，比较难计算，但把根式先化为分数指数幂再计算，这样就简便多了，同样，第(2)小题也是先把根式转化为分数指数幂后再由运算法则计算.

解：(1)原式=

　　　　　　 =

　　　　　　 =

　　　　　　 =

　　　　　　 =

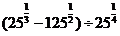
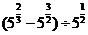
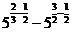
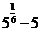
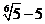
(2)原式=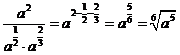

小结：运算的结果不强求统一用哪一种形式表示，但不能同时含有根号和分数指数，也不能既有分母，又含有负指数.

课堂练习：

化简：

(1)

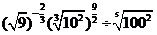
(2)

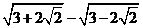
(3)

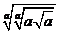
归纳小结：

1．复习分数指数幂的概念与其性质

2．教具：投影仪

1．学法：讲授法、讨论法.

2．难点：有理指数幂性质的灵活应用.

1．重点：运用有理指数幂性质进行化简，求值.

3．情感、态度、价值观

(1)培养学生观察、分析问题的能力；

(2)培养学生严谨的思维和科学正确的计算能力.